Контрольная работа: Теплофизический расчет шара

Введение

Основной целью данного курсового проекта было: найти решение для задачи тепломассопереноса, с использованием различных математических методов. Для решения задачи использовался пакет MathCAD . Для определения эффективности и точности решения поставленной задачи, полученное решение анализируется и определяется оптимальный метод нахождения решения задачи.

1. Постановка задачи

Дан шар 2R, который находится в тепловом равновесии с окружающей средой, т.е. имеет температуру, равную температуре окружающей среды T₀ . В начальный момент времени среда нагревается с постоянной скоростью b (град/сек), т.е. температура среды есть линейная функция времени T_с (t ) = T₀ +bt . Теплообмен между поверхностями пластины и окружающей среды происходит по закону Ньютона. Требуется найти распределение температуры по толщине шара в любой момент времени, а также удельный расход тепла.

Также заданы начальные и граничные условия, которые описываются как:

T(r,0) = T₀ = const,

Дифференциальное уравнение теплопроводности для шара может быть записано как:

2. Решение задачи

Решение задачи было получено для двух материалов: сталь и резина. Основные теплофизические характеристики веществ были сведены в таблицу (см. табл.1)

Таблица 1

Материал	удельная теплоемкость, С (Дж/(кг*К))	плотность тела, ρ(кг/м³)	коэффициент теплопроводности, λ (Вт/м*К)
Сталь	462	7900	45,4
Резина	1380	1200	0,16

Первым шагом в решении задачи было нахождение корней характеристического уравнения:

На основе полученных значений корней характеристического уравнения, для двух материалов построена таблица (табл.2).

Таблица 2

Материал	1	2	3	4	5	6	7	8	9	10	11	12	13
Сталь	0	3.07	6.14	9.21	12.28	15.36	18.44	21.52	24.61	27.70	30.79	33.89	36.98
Резина	0	3.14	6.28	9.42	12.56	15.70	18.84	21.98	25.13	28.27	31.41	34.55	37.69

Найдя корни характеристического уравнения, можно найти безразмерную температуру и температуру тела в любой точке в любой момент времени:

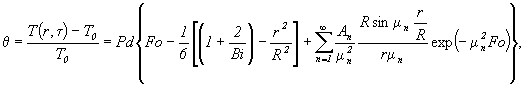
Так как в начальный момент времени, шар только начинает прогреваться, то приведенная выше формула дает большие погрешности. Для уменьшения погрешности используют формулу для нахождения безразмерной температуры для малых значений Фурье:

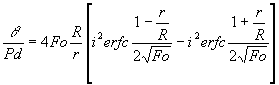
Расчетные формулы имеют следующий вид:

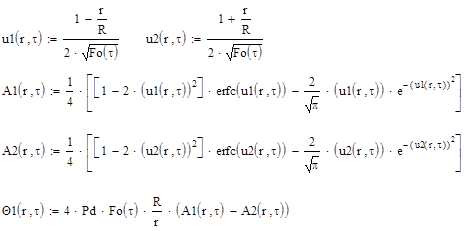Определяем температуру на поверхности и в центре шара:

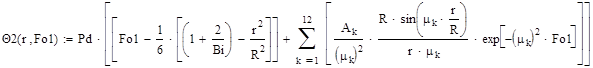
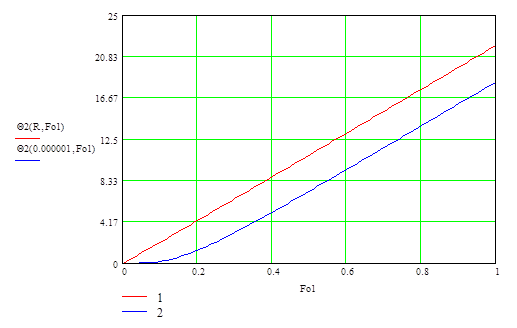
Рис. 1. Зависимость между Θ и Fo для поверхности (1) и центра (2) шара (сталь).

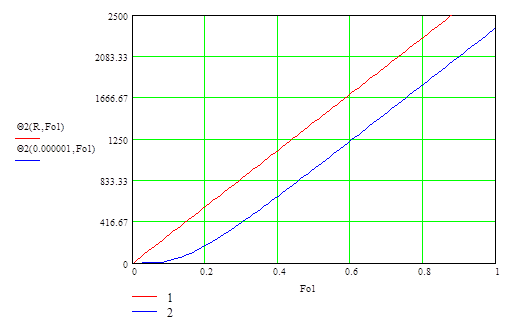
Рис. 2 . Зависимость между Θ и Foдля поверхности (1) и центра (2) шара (резина).

--> ЧИТАТЬ ПОЛНОСТЬЮ <--