Контрольная работа: Теплофизический расчет шара
3. Результаты расчета
Найдя безразмерную температуру во всех точках шара, можно определить температуру в любых точках шара в любой момент времени:
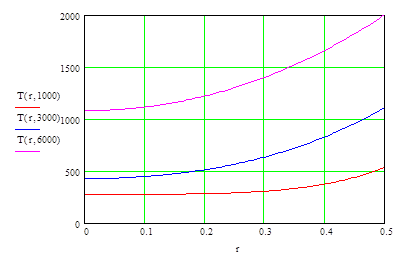 |
Рис. 3 . Распределение температуры по толщине шара (сталь).
Таблица 2 .
| T(r,1000) | 273.64 | 273.64 | 273.65 | 273.67 | 273.68 | 273.71 | 273.74 | 273.78 | 273.82 | 273.87 | 273.92 |
| T(r,3000) | 433.34 | 433.40 | 433.55 | 433.80 | 434.15 | 434.61 | 435.16 | 435.82 | 436.57 | 437.43 | 438.39 |
| T(r,6000) | 1098.8 | 1098.9 | 1099.1 | 1099.5 | 1100.2 | 1100.9 | 1101.9 | 1102.9 | 1104.2 | 1105.7 | 1107.3 |
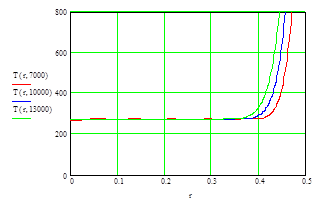
Рис. 4 . Распределение температуры по толщине шара (резина).
Таблица 3 .
| T(r,7000) | 265.54 | 265.54 | 265.55 | 265.55 | 265.56 | 265.57 | 265.59 | 265.60 | 265.62 | 265.64 | 265.67 |
| T(r,10000) | 271.59 | 271.59 | 271.59 | 271.59 | 271.59 | 271.59 | 271.60 | 271.60 | 271.60 | 271.61 | 271.61 |
| T(r,13000) | 272.54 | 272.54 | 272.54 | 272.54 | 272.54 | 272.54 | 272.54 | 272.54 | 272.54 | 272.54 | 272.54 |
Для распределения температуры по толщине шара для различных моментов времени составлены таблицы, для стального (табл. 2) и резинового шара (табл.3).
Построены графики зависимости температуры в различные моменты времени от толщины шара, для стали (рис.3) и резины (рис.4).
Также можно найти температуру в любых точках шара при малых значениях Фурье.
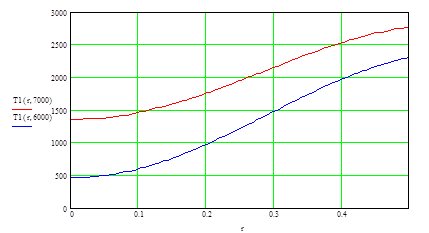
Рис. 5 . Распределение температуры по толщине шара при малых значениях Fo(сталь).
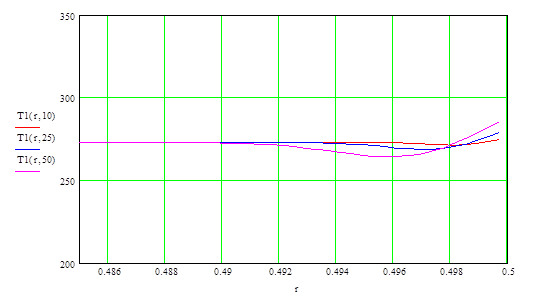
Рис. 6 . Распределение температуры по толщине шара при малых значениях Fo(резина).
По результатам, полученным для малых значений Fo, построены графики распределения температуры по толщине шара, для различных моментов времени, для стали (Рис. 5) и резины (Рис. 6)
Анализ графика распределения температуры по толщине шара при малых значениях Fo для шара из резины (Рис. 6):
Произведем расчет безразмерной температуры для шара из резины при 50 секундах, различными формулами для нахождения безразмерной температуры и сравним их:
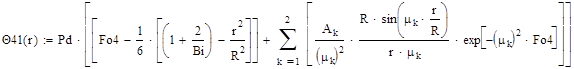
Первая формула (1) определяет избыточную температуру по толщине шара при заданном значении Fo.
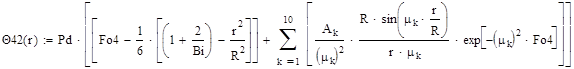
(2)
Вторая формула (2) отличается от первой тем, что в сумму ряда входит 10 членов ряда, что в 5 раз больше, чем в предыдущей.
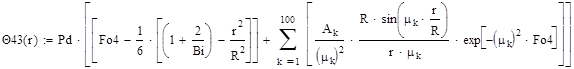 (3)
(3)
В третьей формуле (3) используется 100 членов ряда, что в 50 раз больше, чем в первой формуле.
![]()
Четвертая формула – формула для нахождения избыточной температуры по толщине шара для малых значений Фурье.
По результатам расчета получен график, на котором, для удобства сравнения, объединены все 4 значения избыточной температуры (Рис. 6.1)
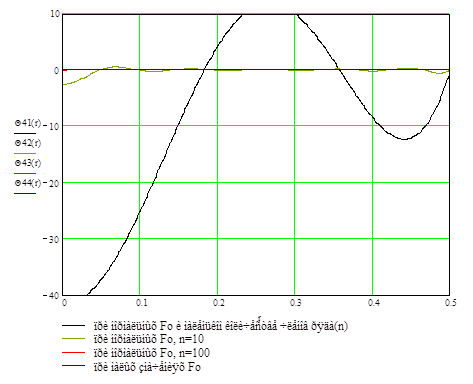
Рис. 6.1 . Распределение температуры по толщине шара (резина).