Контрольная работа: Теплофизический расчет шара
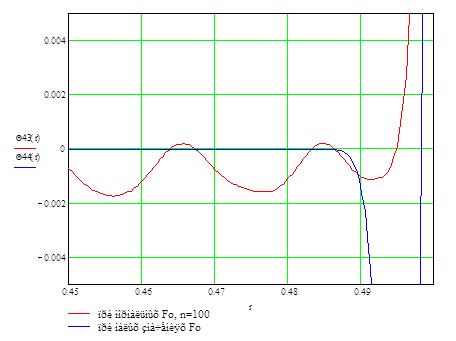
Рис. 6.2 . Распределение температуры по толщине шара (резина).
Использование формулы (3) дает большую точность решения, но в узко ограниченной области толщины шара(r=0.485-0.5м), на остальном промежутке значений радиуса шара погрешность формулы (3) гораздо больше формулы (4).
Проверим точность этих формул, задав точку радиуса шара вблизи поверхности (r=0.495м), варьируя значении параметра Фурье от 0 до 1.
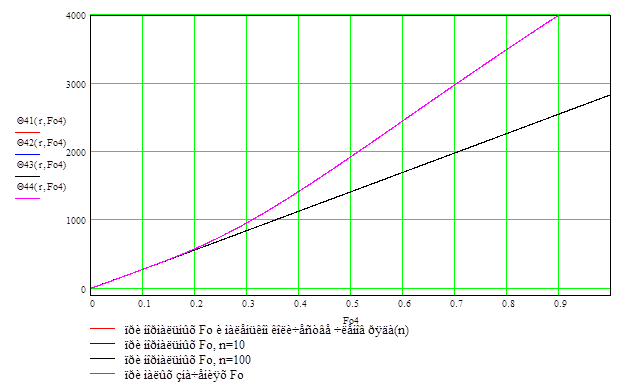По результатам расчетов построен график зависимости избыточной температуры от параметра Фурье (Рис. 6.3).Также построен еще один график зависимости избыточной температуры от параметра Фурье, но в более ограниченной области (Рис. 6.4).
Рис. 6.2 . Зависимости Θ от Fo (резина).
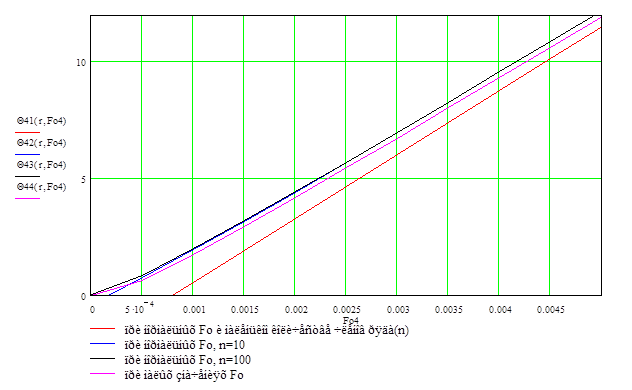Рис. 6. 3 . Зависимости Θ от Fo (резина).
Распределение температуры по толщине шара из стали (табл. 4) и резины (табл.5), в различные моменты времени, сведены в таблицы.
Таблица 5 . Распределение температуры для шара из стали
| r | 0 | 0.05 | 0.1 | 0.15 | 0.2 | 0.25 | 0.3 | 0.35 | 0.4 | 0.45 | 0.5 |
| T(r,6000) | 460.30 | 495.29 | 597.74 | 760.37 | 971.55 | 1216.1 | 1476.5 | 1733.3 | 1968.7 | 2163.5 | 2302.2 |
| T(r,6500) | 899.89 | 931.29 | 1023.2 | 1168.9 | 1358.0 | 1576.6 | 1808.6 | 2036.8 | 2243.6 | 2412.5 | 2528.8 |
| T(r,7000) | 1350.5 | 1378.4 | 1459.8 | 1588.9 | 1755.9 | 1948.6 | 2152.3 | 2351.3 | 2529.6 | 2672.0 | 2765.2 |
| T(r,7500) | 1806.5 | 1830.9 | 1902.2 | 2015.1 | 2160.8 | 2328.3 | 2504.3 | 2674.5 | 2824.6 | 2940.6 | 3010.1 |
Таблица 6 . Распределение температуры для шара из резины
| r | 0 | 0.05 | 0.1 | 0.15 | 0.2 | 0.25 | 0.3 | 0.35 | 0.4 | 0.45 | 0.5 |
| T(r,300) | 273.00 | 273.00 | 273.00 | 273.00 | 273.00 | 273.00 | 273.00 | 273.00 | 273.00 | 273.00 | 361.31 |
| T(r,600) | 273.00 | 273.00 | 273.00 | 273.00 | 273.00 | 273.00 | 273.00 | 273.00 | 273.00 | 272.97 | 450.62 |
| T(r,1000) | 273.00 | 273.00 | 273.00 | 273.00 | 273.00 | 273.00 | 273.00 | 273.00 | 273.00 | 270.29 | 569.94 |
| T(r,2000) | 273.00 | 273.00 | 273.00 | 273.00 | 273.00 | 273.00 | 273.00 | 273.00 | 272.98 | 180.45 | 868.71 |
4. Анализ решения
Из уравнения:
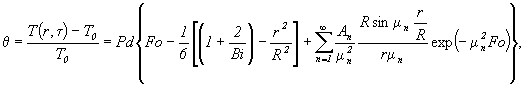
видно, что относительная избыточная температура прямо пропорциональна критерию Pd, т. е. скорость нагревания окружающей среды непосредственно влияет на повышение температуры тела в любой его точке.
Ряд в решении быстро сходится, и поэтому для квазистационарного режима, определяемого условием Fo>Fo1, им можно пренебречь.
При Bi →∞ температура поверхности шара будет линейной функцией времени. решение для безразмерной температуры можно записать в виде:
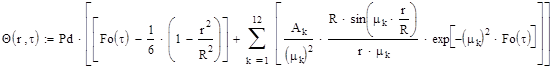
С
делав оценку ряда для центра шара (r=0), решение можно записать как:
где
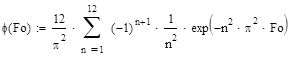
Используя эти уравнения можно найти количество членов ряда, необходимое для получения точного решения:
,
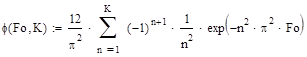
где К - количество членов ряда
 |
Рис. 7 .Зависимость суммы ряда от количества членов ряда
Таблица 7 .
| φ(0.01,K) | 1.1016 | 0.8968 | 0.9523 | 0.9367 | 0.9408 | 0.9398 | 0.9400 | 0.9399 | 0.9400 | 0.94 |
| φ(0.05,K) | 0.7422 | 0.7000 | 0.7015 | 0.7016 | 0.7016 | 0.7016 | 0.7016 | 0.7016 | 0.7016 | 0.7016 |
| φ(0.1,K) | 0.4532 | 0.4473 | 0.4473 | 0.4473 | 0.4473 | 0.4473 | 0.4473 | 0.4473 | 0.4473 | 0.4473 |
| φ(0.5,K) | 0.0087 | 0.0087 | 0.0087 | 0.0087 | 0.0087 | 0.0087 | 0.0087 | 0.0087 | 0.0087 | 0.0087 |
Можно получить график зависимости величины суммы ряда для различных значений числа Фурье от количества членов ряда(Рис. 7). А также составить таблицу значений величины суммы ряда (табл. 7).