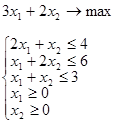Контрольная работа: Умножение матрицы. Теория вероятности

106,114,05

121,65

129,25

136,85

144,45

8

13

11

6

0

2

Хср = ∑х/n,

Если данные собраны в вариационный ряд, то среднее можно получить как:

Хср = FXi / n =

8×106,4+13×114,05+11×121,65+6×129,25+0×136,85+2×144,45 / 40 = 118,4, Х ср = 118,4.

2 2 2 2 2 2 2 2

S = ∑FXi - (∑FXi) / n = 8×106,4+13×114,05+11×121,65+6×129,25+0×136,85+2×144,45 -

2

- 1 / n (8×106,4+13×114,05+11×121,65+6×129,25+0×136,85+2×144,45) = 564414,84 – 560837,124 = 3577,7;

S = 3577,7.

2

Варианта = S / n-1;

2

Вар. = √Вар, Вар.= √3577,7 / 39 = 9,6;

Доверительный интервал - границы прогноза

Хср - t × вар. / √n < Xср. ген. < Хср + t × вар. / √n;

По таблице:

Для n = 40 при вероятности р = 0,95 значение t - критерия Стьюдента = 2,022;

При р = 0,99, t = 2,708

Для р = 0,95:

118,4 - 2,022 × 9,6/√40 < Хср. ген. < 118,4+2,022 × 9,6/√40,115,3 < Хср. ген. < 121,5, 118,4 ± 3,1, Для р = 0,99:

118,4 - 2,708 × 9,6/√40 < Хср. ген. < 118,4+2,708 × 9,6/√40,114,3 < Хср. ген. < 122,5, 118,4 ± 4,1

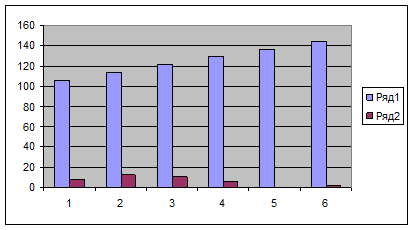
Задание 7

Решить задачу линейного программирования.