Контрольная работа: Универсальная тригонометрическая подстановка

,

где , ,…, , . Найдем общий знаменатель дробей ,…, . Пусть это число . Сделаем подстановку , . В этом случае все дробные степени становятся целыми и подынтегральная функция становится рациональной относительно .

2. Рассмотрим общий случай подобных интегралов:

,

где , ,…, , .

Чтобы получить рациональную функцию, находят общий знаменатель дробей ,…, (обозначим его ) и делают замену переменной . В этом случае

.

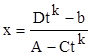
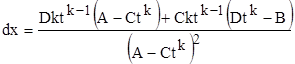Очевидно, если и , то случай 2 переходит в случай 1. Кроме того, необходимо иметь в виду, что в обоих случаях основания всех степеней должны быть одинаковы: в первом случае , во втором – .

4. Интегрирование некоторых иррациональных функций с помощью тригонометрических подстановок

Рассмотри снова интегралы, содержащие квадратный трехчлен:

.

Выделив полный квадрат под корнем, получим один из трех интегралов: , , . Все они вычисляются с помощью тригонометрических подстановок.

1.

.

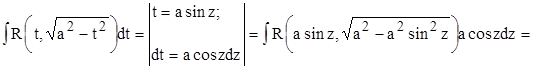
2.

.

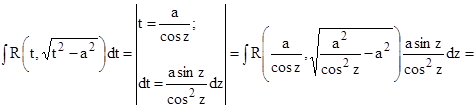
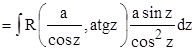3.

.

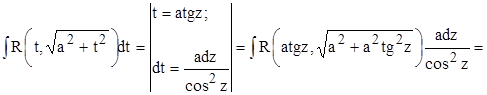
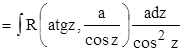Во всех трех случаях после проведенных подстановок интегралы пришли к виду, рассмотренному в п. 2.

5. Интегралы, не выражающиеся через элементарные функции

В п. 1 была сформулирована теорема о том, что любая непрерывная функция имеет первообразную. Однако необходимо иметь в виду, что не всегда первообразная выражается в конечном виде через элементарные функции.

К таким интегралам следует отнести

, , , ,

().

Во всех подобных случаях первообразная представляет собой некоторую новую функцию, которая не сводится к комбинации конечного числа элементарных функций.

Например, та из первообразных , которая обращается в нуль при , называется функцией Гаусса и обозначается . Эта функция хорошо изучена, составлены подробные таблицы ее значений. То же самое можно сказать и о других подобных функциях.

Литература

1. Александров В.В., Потапов М.К., Пасиченко П.И., Потапов М.К. Александров В.В., Потапов М.К и др. Алгебра, тригонометрия и элементарные функции. Учебник. М: Высшая школа, 2001. – 736 с.