Дисперсия (Д):

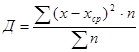
Инструмент А
Год	Норма дохода	хср		Д	σ		ν
1	9	11		12	3,46410162		31,4918329
2	9
3	15
Инструмент Б
Год	Норма дохода	хср	Д			σ	ν
1	13	13,7	9,33			3,05505046	22,3540278
2	11
3	17
Инструмент В
Год	Норма дохода	хср		Д	σ		ν
1	23	24,3		1,33	1,15470054		4,74534468
2	25
3	25
Инструмент АБ
Год	Норма дохода	хср		Д	σ		ν
1	11	12,3		10,3	3,21455025		26,063921
2	10
3	16
Инструмент БВ
Год	Норма дохода	хср		Д	σ		ν
1	18	19		3	1,73205081		9,11605688
2	18
3	21
Инструмент АВ
Год	Норма дохода	хср		Д	σ		ν
1	12	13,2		1,08	1,040833		7,90506076
2	13,5
3	14

Сгруппируем полученные данные по коэффициенту вариации, т.е. по степени риска.

Слабая вариация, низкий риск (ν до 10%)	Умеренный риск (ν = 10 … 25%)	Высокий риск (ν свыше 25%)
В = 4,7; БВ = 9,11; АВ = 7,9	Б=22,35	А=31,49; АБ=26

Если предприниматель должен выбрать один из финансовых инструментов А, Б, или В (стратегия а), то наименее рискованным для него будет инструмент В (коэффициент вариации 4,7%).

Если предприниматель может составить портфель из этих инструментов, то наименее рискованным является портфель АВ, включающий 50% инструмента А и 50% инструмента В.

Задача 5. X=2

В портфеле предприятия "Сибин" находятся два вида акций с разными среднегодовыми нормами доходности – акции "А" и акции "Б" с соответствующими характеристиками абсолютного размера риска в виде среднеквадратических отклонений σ (А) и σ (Б). Коэффициент корреляции текущих норм доходности акций "А" и "Б" равен: –1.

Среднегодовая норма доходности		Абсолютный размер риска
акции А	акции Б	σА	σБ
11	15,5	4,95	13,8

Найти пропорцию распределения денежных средств, инвестируемых в акции, соответствующие минимуму риска (нулевой дисперсии).

Известно, что коэффициент корреляции равен –1. Данный коэффициент рассчитывается по формуле:

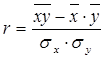, (1)

где х и y – зависимые величины. В нашем случае это нормы доходности акций А и Б, т.е.:

= 11

= 15,5

Подставим значения этих величин в формулу коэффициента корелляции:

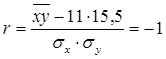
Выразим :

Значит средняя величина произведений норм доходности акций А и Б равна 102,19.

При распределении денежных средств, соответствующим минимуму риска, дисперсия стремится к нулю.

Выразим из формулы (1) произведение σ_А σ_Б и приравняем к нулю.

= 0

Значит распределение средств должно быть таким, чтобы произведение средних норм доходности акций было равно 102,19.

Список литературы

1. Романов В.С. Понятие рисков и их классификация как основной элемент теории рисков // Инвестиции в России. — 2000г. — № 12, с. 41—43

2. Романов В.С., Бутуханов А. В. Рискообразующие факторы: характеристика и влияние на риски // Управление риском. — 2001 г. № 3, с.10—12.

3. Романов В. С. Риск-менеджмент как условие развития предприятия. Теория и практика реструктуризации предприятий: Сборник материалов Всероссийской научно-практической конференции. Пенза, 2001 г. — с.144—146.

4. Романов В. С. Управление рисками: этапы и методы // Факты и проблемы практики менеджмента: Материалы научно-практической конференции 30 октября 2001 г. — Киров: Изд-во Вятского ГЛУ, 2001 г. — с. 71—77.

5. Станиславчик Е. Н. Риск-менеджмент на предприятии. Теория и практика. М.: "Ось-89", 2002. – 80 с..