Контрольная работа: Вычисление вероятности

Дисперсию определим по формуле: .

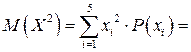
= 24,55.

Тогда

Найдем функцию распределения случайной величины.

.

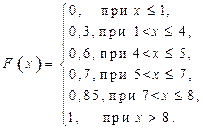
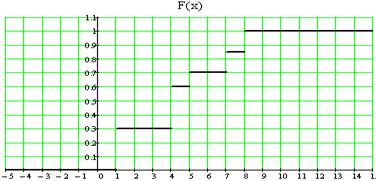
Построим график этой функции

6. Задача 6. Случайная величина задана плотностью вероятности

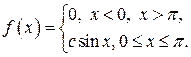
Определить константу , математическое ожидание, дисперсию, функцию распределения величины , а также вероятность ее попадания в интервал [0;]

Решение.

Коэффициент найдем используя свойство функции плотности распределения: 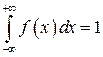. Так как функция плотности распределения принимает отличные от нуля значения на интервале , то .

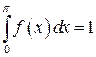Вычислим определенный интеграл:

.

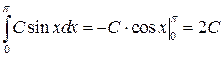Следовательно, , .

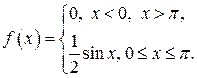
Математическое ожидание найдем по формуле:

.

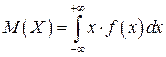Т.к. плотность распределения принимает отличное от нуля значения только на отрезке [0, ], то

= =

= = .

Вычислили интеграл, используя формулу интегрирования по частям.

Найдем дисперсию , т.к. плотность распределения принимает отличное от нуля значения только на отрезке

[0, ], то .

=.

Найдем .

Воспользуемся формулой =.