Контрольная работа: Застосування подвійних інтегралів

Рисунок 1 - Область: а ) ; б)

подвійний інтеграл полярна координата

Якщо область охоплює початок координат, тобто точка є внутрішньою точкою області , то

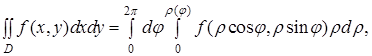(6)

де - полярне рівняння межі області .

Приклади

1. Обчислити інтеграл , якщо область - паралелограм,

обмежений прямими (рис.1, а ).

Розв’язання

Безпосереднє обчислення цього інтеграла надто громіздке, тому що як в напрямі осі так і в напрямі осі область потрібно спочатку розбити на три області, а потім обчислювати три подвійних інтеграли.

Виконаємо таку заміну змінних: , тоді прямі та в системі переходять в прямі та у системі (рис.1, б), а прямі та відповідно в прямі та .

Таким чином, область (паралелограм) переходить у системі в прямокутник .

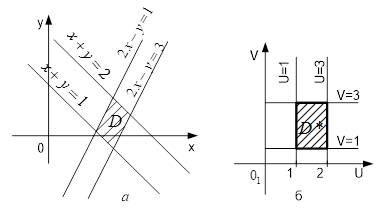
Рисунок 2 - Область: а ) ; б)

Далі маємо

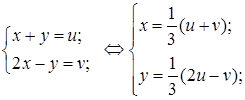
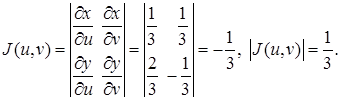
За формулою (3)

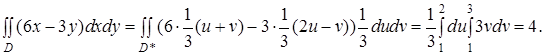
2. У подвійному інтегралі , де - круг, обмежений колом , перейти до полярних координат з полюсом в точці , і обчислити отриманий інтеграл.

Розв’язання

Область зображена на рис.2.

Рівняння, які пов’язують і полярні координати з полюсом у точці , мають вигляд , причому видно, що кут змінюється в межах віддо .

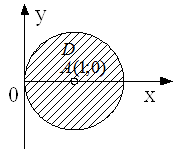
Рисунок 3 - Область

Підставивши вирази для і в рівняння кола, отримаємо , звідки або . Ці дві криві на площині при обмежують область , яка є прообразом області при відображенні. Якобіан відображення дорівнює . Підінтегральна функція у нових змінних дорівнює . За формулою (3) маємо

.

Одержаний подвійний інтеграл за областю зводимо до повторного: