2. Застосування подвійних інтегралів до задач геометрії

1. Площа плоскої фігури. Якщо в площинізадана фігура, щомає форму обмеженої замкненої області,то площа цієї фігури знаходиться, як відомо, за формулою:

.

2. Об'єм тіла. Об'єм циліндричного тіла, твірні якого паралельні осі і яке обмежене знизу областю площини , а зверху - поверхнею , де функція неперервна та невід'ємна в області , знаходиться за формулою (2):

3. Площа поверхні. Якщо поверхня ,задана рівнянням

(7)

проектується на площину в область ( рис.3) і функції , , неперервні в цій області, то площу поверхні знаходять за формулою

(8)

Рисунок 4 - Поверхня

Виведемо цю формулу. Розіб’ємо довільним способом область на частин , які не мають спільних внутрішніх точок і площі яких дорівнюють . У кожній частині візьмемо точку ; на поверхні їй відповідатиме точка , де . Через точку проведемо дотичну площину [3]

.

На площині виділимо ту її частину, яка проектується на площину в область . Позначимо цю частину дотичної площини через , а її площу - через . Складемо суму

. (9)

Границю суми (9), коли найбільший з діаметрів областей прямує до нуля, назвемо площею поверхні ( 7), тобто за означенням покладемо

. (10)

Обчислимо цю границю. Оскільки область , яка має площу , проектується в область з площею , то , де - кут між площинами та ( рис.3), тому .

Але гострий кут дорівнює куту між віссю і нормаллю до дотичної площини, тобто куту між векторами та . Знайдемо за формулою (4)

.

Отже,

.

Підставляючи значення в (10), отримуємо

.

Під знаком границі маємо інтегральну суму, складену для неперервної в області функції . Ця функція інтегровна в області , тому границя у формулі (10) існує і дорівнює подвійному інтегралу (8).

3. Застосування подвійних інтегралів до задач механіки

1. Маса пластини. Нехай на площині маємо матеріальну пластину, яка має форму обмеженої замкненої області , в кожній точці якої густина визначається неперервною функцією . Маса такої пластини визначається за формулою (1.8):

.

2. Центр маси пластини. Статичні моменти. Нехай матеріальна пластина в площині має форму області , густина пластини в точці дорівнює , де - неперервна функція в області Розіб'ємо область на частини ,виберемо в кожній з них довільну точку і наближено вважатимемо, що маса частини дорівнює , де - площа області . Коли вважати, що кожна з цих мас зосереджена в точці , то пластину можна розглядати як систему цих матеріальних точок. Тоді координати та центра маси пластини наближено визначатимуться рівностями

.
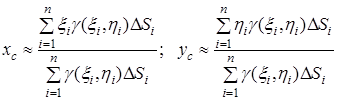