Контрольная работа: Застосування подвійних інтегралів

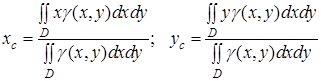. (11)

Величини

(12)

називаються статичними моментами пластини відносно осі та .

Враховуючи формули (8), (11) і (12), координати центра мас можна записати у вигляді

.

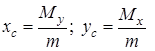Якщо пластина однорідна, тобто має сталу густину , то у формулах (1.8), (11) і (12) слід покласти .

3. Моменти інерції пластини. Відомо, що момент інерції матеріальної точки відносно деякої осі дорівнює добутку маси точки на квадрат її відстані від цієї осі, а момент інерції системи матеріальних точок відносно однієї і тієї самої осі дорівнює сумі моментів інерції всіх точок системи.

Нехай матеріальна пластина має форму області у площині ,а неперервна функція визначає густину в кожній точці цієї пластини. Розіб'ємо область на частини , площі яких дорівнюють , і виберемо в кожній з цих частин довільну точку . Замінимо пластину системою матеріальних точок з масами . Якщо пластину розглядати як систему цих матеріальних точок, то моменти інерції пластини відносно осі та відносно наближено визначатимуться за формулами

.

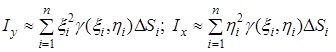Перейшовши до границі в кожній із сум при , отримуємо точні формули для обчислення моментів інерції розглядуваної пластини відносно координатних осей:

. (13)

Знайдемо момент інерції пластини відносно початку координат.

Враховуючи, що момент інерції матеріальної точки з масою відносно початку координат дорівнює , аналогічно отримуємо, що

. (14)