Застосування подвійних інтегралів

Содержание

1. Заміна змінних у подвійному інтегралі. Подвійний інтеграл у полярних координатах

2. Застосування подвійних інтегралів до задач геометрії

3. Застосування подвійних інтегралів до задач механіки

1. Заміна змінних у подвійному інтегралі. Подвійний інтеграл у полярних координатах

Нехай функція неперервна в деякій замкненій і обмеженій області ,тоді існує інтеграл

.

Припустимо, що за допомогою формул

(1)

ми переходимо в інтегралі до нових змінних та . Вважатимемо, що з формул (1) однозначно можна визначити та :

. (2)

Згідно з формулами (2), кожній точці ставиться у відповідність деяка точка на координатній площині з прямокутними координатами і .

Нехай множина всіх точок утворює обмежену замкнену область . Формули (1) називаються формулами перетворення координат, а формули (2) - формулами оберненого перетворення.

Справедлива така теорема.

Теорема. Якщо перетворення (2) переводить замкнену обмежену область в замкнену обмежену область і є взаємно однозначним, і якщо функції (1) мають в області неперервні частинні похідні першого порядку і відмінний від нуля визначник

, (3)

а функція неперервна в області , то справедлива така формула заміни змінних

. (4)

Функціональний визначник називається визначником Якобі або якобіаном.

Таким чином, виконуючи заміну змінних в інтегралі за формулами (1), ми маємо елемент площі в координатах замінити елементом площі в координатах і стару область інтегрування замінити відповідною їй областю .

Розглянемо заміну декартових координатполярнимиза відомими формулами. Оскільки

.

То формула (3) набирає вигляду

(4)

де область задана в декартовій системі координат , а - відповідна їй область в полярній системі координат.

У багатьох випадках формулу (4) доцільно застосовувати тоді, коли підінтегральна функція або рівняння границі області містить суму , оскільки ця сума в полярних координатах має досить простий вигляд:

.

Якщо область (рис.1, а ) обмежена променями, які утворюють з полярною віссю кути та і кривими та , то полярні координати області змінюються в межах , (рис.1, б). Тому формулу (4) можна записати у вигляді

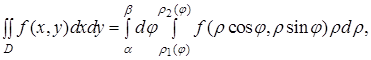(5)

--> ЧИТАТЬ ПОЛНОСТЬЮ <--