Курсовая работа: Аналитическая химия
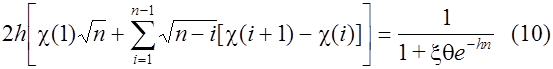
Рейнмут [8] выразил (5) в виде ряда:
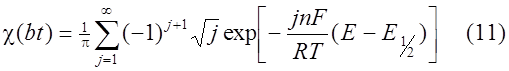
Найденная любым из приведенных способов функция определяет форму вольтамперных кривых в случае обратимого электродного процесса. Уравнение тока пика легко получили на основе уравнения (7) и графика функции (8 - 11). Это выражение известно как уравнение Рендлса - Шевчика:
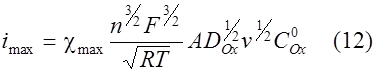
В случае > 6 во всех решениях max = 0.447. Для температуры 25 °С это выражение сводится к зависимости
![]()
Левая полуширина пика, используемая как критерий обратимости, в этой модели для обратимого процесса составляет 0.056/n, В.
Делахеем и Берзинсом [9] была найдена функция, определяющая форму вольтамперной кривой в случае обратимого растворения объемного осадка металла (активность осадка принимается равной 1). В этом случае краевое условие принимает вид
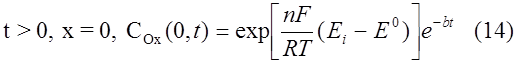 Выражение для тока выглядит как
Выражение для тока выглядит как
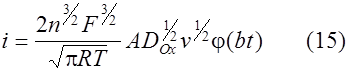 , где
, где 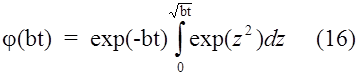
z является вспомогательной переменной. Функция (16) имеет максимум, равный 0.541 при bt = 0.924. Соответствующий ток пика при 25 °С составляет
![]()
Левая полуширина пика в этой модели для обратимого процесса составляет 0.016n, В.
Никольсон [11] установила зависимость i(E) для растворения отдельного незаполненного монослоя металла с поверхности плоского электрода. При этом уравнение Нернста записывается как

a = m/ms (19)
a - активность осадка
m - количество металла на электроде,
ms - количество металла на единицу активности,
f - коэффициент активности,
Еp - равновесный потенциал, соответствующий а0 и с0
Активность а является в данном случае функцией времени

Схема решения такая же, как и в предыдущем случае. Уравнение вольтамперной кривой в интегральной форме в этой модели выглядит так:


Точки первой производной (bt) описывают форму кривой i(E) и
i = nFm0b(bt) (23)
Это уравнение эквивалентно уравнению