Курсовая работа: Аналіз чутливості використання методу Якобі для рішення задач лінійного програмування

Описана вище процедура складає основу так називаного методу множників Лагранжа, що дозволяє ідентифікувати стаціонарні крапки при рішенні оптимізаційних задач з обмеженнями у виді рівностей. Схему цього методу можна формально представити в такий спосіб. Нехай

L(x,)= (x, ) - g(x) .

Функція L називається функцією Лагранжа. Параметри звуться множників Лагранжа і, як випливає з визначення, мають той же зміст, що і коефіцієнти чутливості описані вище. Рівняння

і

виражають розглянуті вище необхідні умови наявності єкстремуми, що породжуються функцією Лагранжа безпосередньо. Це означає, що задача оптимізації з цільовою функцією f(x) при наявності обмеження g(х)=0 еквівалентна задачі перебування безумовного єкстремуми функції Лагранжа

L(x, ). Достатні умови, використовувані при реалізації методу множників Лагранжа, формулюються нижче без доказу. Визначимо матрицю

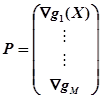, де і 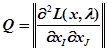для всіх i і J

=+

Матриця Н^B являє собою так називану облямовану матрицю Гессе.

Нехай дана стаціонарна крапка (х₀ , ₀₎ функції Лагранжа L (х, ), а облямована матриця Гессе Н^В сформована зі значень відповідних елементів у крапці (Хо, ₀ ). Тоді Х₀ є:

1) крапкою максимуму, якщо, починаючи з головного мінору порядку (m+l), наступні (n-m) головних мінорів матриці Н^В утворять знакоперемінний числовий ряд, знак першого члена якого визначається множником ,(-1)^м+1 ;

2) крапкою мінімуму, якщо, починаючи з головного мінору порядку (m+1), знак наступних (n-m) головних мінорів матриці Н^В визначається множником (-1)^м. Сформульовані умови виявляються достатніми для ідентифікації екстремальної крапки, але не є необхідними. Іншими Словами, стаціонарна крапка, що не задовольняє цим умовам, може бути екстремальною. Існують інші умови для ідентифікації екстремальних крапок, що є як необхідними, так і достатніми. Однак практичне використання цих умов у ряді випадків зв'язано зі значними обчислювальними труднощями. Визначимо матрицю

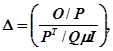
утворену значеннями відповідних функцій у стаціонарній крапці (Хо, ₀ ). Тут µ - невідомий параметр, а Р и Q визначені вище. Нехай | |-визначник матриці ; тоді кожний з (n-m) дійсних коренів і i полінома | |=0 повинний бути:

1)негативним, якщо хо - крапка максимуму;

2)позитивним, якщо хо- крапка мінімуму.

Один з методів, що іноді застосовуються для рішення систем рівнянь, що виражають необхідні умови наявності екстремуми, полягає в послідовному виборі числових значень , після реалізації, якого дана система зважується відносно х.

3. ВИКОРИСТАННЯ МЕТОДУ ЯКОБІ ДЛЯ РІШЕННЯ ЗАДАЧ ЛІНІЙНОГО ПРОГРАМУВАННЯ

Дано задачу лінійного програмування, у якій потрібно максимізувати z=2xi+3xa

при обмеженнях х₁ +х₂ +х₃ =5

х_1-х2 +х₄ =3

х₁ ,х₂ ,х₃ ,х₄ > 0

Розглянемо обмеження x_j > 0 устанавлюючи не заперечність перемінних. Нехай W_J ² - відповідна (ненегативна) додаткова перемінна. При цьому x- W_J ² чи x=W_J ² .Така заміна робить надлишковим умову не заперечності перемінних, і вихідна задача приймає наступний вид:

максимізувати z=2W₁ ² +3W₂ ²

при обмеженнях W₁ ² +W₂ ² +W₃ ² =5,

W₁ ² -W₂ ² +W₄ ² =3.

Щоб застосувати метод Якобі, покладемо

Y=(W₁ ,W₂ ) і Z=(W₃ ,W₄ ).

(Помітимо, що вектори Y і Z, якщо використовувати термінологію лінійного програмування, утворені базисними і небазисними перемінними відповідно). Маємо

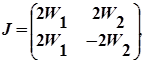
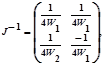W₁ і W₂ 