Курсовая работа: Аналіз чутливості використання методу Якобі для рішення задач лінійного програмування

Отримана система містить (m+1) рівнянь з (n+1) невідомими, котрими є і . Невідому величину можна визначити, якщо знайдений вектор . Це означає, що в нас мається m рівнянь з n невідомими.

Якщо m>n то принаймні (m-n) рівнянь виявляються надлишковими. Після усунення надмірності кількість незалежних рівнянь у системі стає рівним m<n. У випадку коли m=n рішення тривіальне: =0. При цьому крапка X не має припустимої околиці, і, отже, простір рішень складається з єдиної крапки. Така ситуація не представляє інтересу. Випадок, що залишився, коли m<n, необхідно розглянути докладно. Нехай X(Y,Z), де Y=(y₁ ,y₂ ,…,y_m )і Z=(z₁ ,z₂ ,…,z_n-m )є відповідно залежний і незалежний перемінний, утворюючий вектор Х. У нових позначеннях градієнти функцій  і g мають наступний вид:

Уведемо визначення двох матриць:

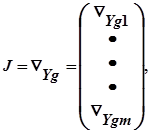
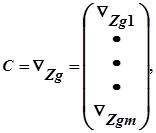
Матрицю J_mxm : називають матрицею Якобі, а C_{mx (n-m)} -матрицею керування. Передбачається, що матриця Якобі J невирождена. Цей факт завжди має місце, оскільки m рівнянь незалежні по визначенню. Отже, компоненти вектора J можна вибрати серед компонентів X таким чином, що матриця J виявиться невирожденою.

Використовуючи дані вище визначення, перепишемо вихідну систему рівнянь з невідомими й у наступному виді:

Тому що матриця J— невирождена, існує зворотна матриця J^-1 . Отже,

Ці рівняння визначають як функцію (нагадаємо, що Z є вектором незалежних перемінних). Заміна в рівнянні дозволяє виразити через :

З цього рівняння випливає, що диференціювання функції по векторі незалежних перемінних Z дає формулу:

де -приведений градієнт функції. Вектор (Y,Z) повинний звертатися в нуль у стаціонарних крапках.

Достатні умови наявності єкстремуми в стаціонарній крапці аналогічні умовам, представленим у розділі. 1.1. У цьому випадку елементи матриці Гессе відповідають компонентам вектора незалежних перемінних Z і є приведеними другими похідними, які можна обчислити, скориставшись рівністю:

Вектор задає i-ю рядок (приведеної) матриці Гессе. Помітимо, що W є функцією Y, а Y— функцією Z; при цьому

Таким чином, при обчисленні частинної похідної по z_i , варто застосувати до компонентів W правило диференціювання складної функції. Це означає, що

5. ІНДИВІДУАЛЬНЕ ЗАВДАННЯ

5.1. Постановка задачі.

Розглядається наступна задача:

максимізувати X=x1² +2x2² +10x3² +5x1x2,

при