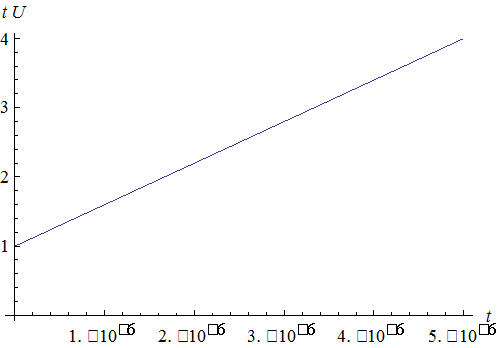Курсовая работа: Анализ избирательных цепей в частотной и временной областях Расчет отклика
Принуждённую составляющую 
находим в установившемся режиме, при 
,когда сопротивление ёмкости Cравно бесконечности и она представляет собой разрыв цепи.
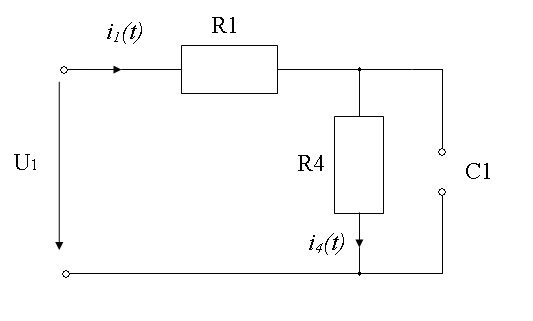
Рисунок 1.1- Состояние схемы для
Коэффициент A найдём из уравнения (1.5) для момента времени t (+0) , воспользовавшись нулевыми начальными условиями 
.
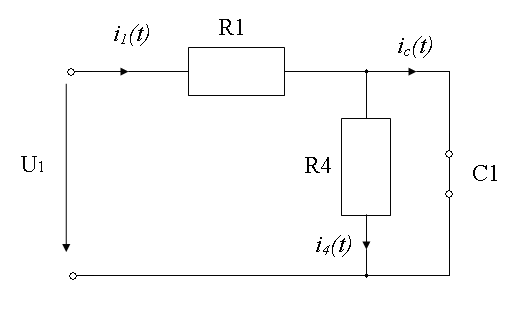
Рисунок 1.2- Состояние схемы для 
Резистор R 4 шунтируется ёмкостью С и ток i 4 (+0)=0.
Из последнего уравнения находим A:
Подставим это выражение в (1.5) и получим формулу переходной характеристики:
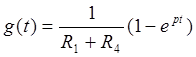(1.6)
Подставляем числовые значения:
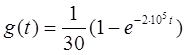
Импульсную характеристику h ( t ) рассчитываем по формуле:
(1.7)
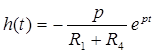(1.8)
Окончательная формула h(t) :
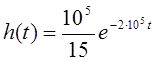
Таблица 1.1-Мгновенные значения h ( t ) и g ( t ) .
| t, мкс | 0 | 1 | 2 | 5 | 10 | 15 | 20 | 25 |
| g(t) *10-3 См | 0 | 6.042 | 10.989 | 21.070 | 28.822 | 31.673 | 32.722 | 33.108 |
| h(t), См | 6666.67 | 5458.21 | 4468.8 | 2452.53 | 902.235 | 331.914 | 122.104 | 44.919 |
Графики переходной и импульсной характеристик изображены на рисунках 1.3 и 1.4 соответственно.
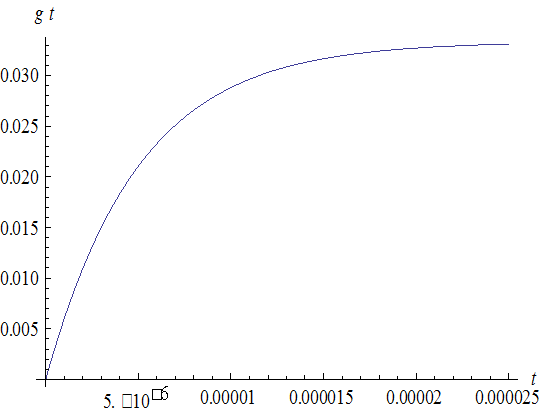
Рисунок 1.3- График переходной характеристики
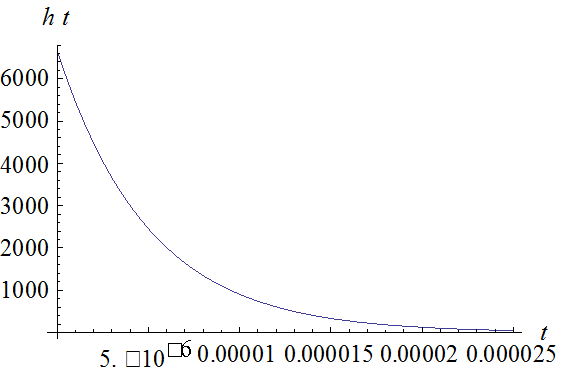
Рисунок 1.4- График импульсной характеристики
2 Расчет отклика цепи интегралом Дюамеля
График входного воздействия U ( t ) показан на рисунке 2.1.
