Курсовая работа: Анализ избирательных цепей в частотной и временной областях Расчет отклика

Восстанавливаем функцию U ( t ) по графику при помощи формулы для прямой, проходящей через 2 точки:

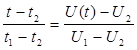(2.1)

Подставляем значения из графика, выражаемU ( t ) из уравнения и получаем:

(2.2)

Для расчета отклика цепи y ( t ) воспользуемся интегралом Дюамеля:

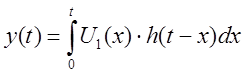(2.3)

где U ₁ ( x ) – входное воздействие, U ₁ ( x )= U ( t ) , если x=t.

Подставляем выражения для U ₁ ( x ) и для h ( t ) в (2.3):

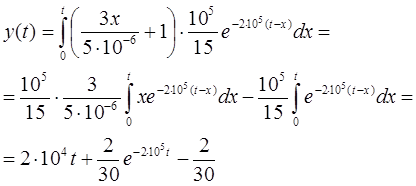
Окончательное выражение для отклика цепи на воздействие U ( t ) :

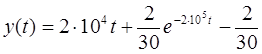(2.4)

Таблица 2.1 - Мгновенные значения отклика цепи

t, мкс	0	1	2	5	10	15	20	25
i4 (t), мА	0	7.91	18.02	57.85	142.3	236.6	334.5	433.7

График y ( t ) приведен на рисунке 2.2.

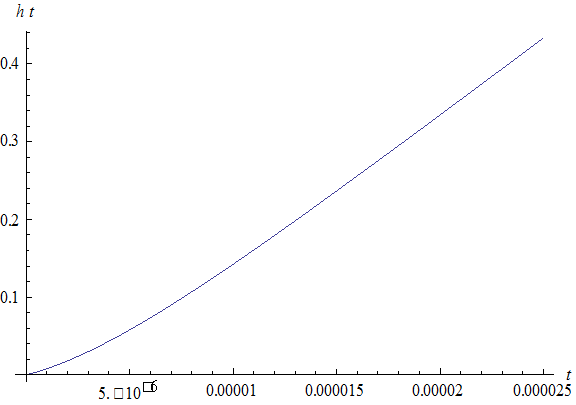
Рисунок 2.2- График отклика цепи

3 Расчет частотных характеристик схемы операторным методом

Найдём ОПФ цепи как отношение изображения отклика I ₄ ( p ) к изображению воздействия U ₁ ( p ) :

(3.1)

Применяя формулу разброса токов, находим отклик в операторном виде:

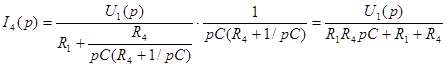
Тогда операторная характеристика:

(3.2)

Заменяя в (3.2) комплексную переменную p на jw , получаем КПФ цепи:

(3.3)

(3.4)

Для определения АЧХ находим модуль КПФ:

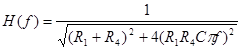(3.5)

(3.6)

Для определения ФЧХ находим аргумент КПФ: