Курсовая работа: Анализ методов государственного регулирования налогообложения и их влияние на производство и потребление

В стоимостных балансах (17 - 21) использованы ставки налога на единицу продукции t0,t1,t2 . Но можно расчетным путем перейти к подушному принципу исчисления налогов на одного занятого по секторам примут вид:

(22)

где Xi, Li, Ki – выпуск продукции, число занятых и ОПФ i-го сектора, при этом выпуск Xi задается как линейно-однородная производственная функция , L – общее число занятых в производственной сфере.

Общий объем сбора налогов

(23)

Средний сбор налогов на одного занятого

(24)

Управляющее воздействие государства в налоговой политике состоит в изменении налоговых ставок от первоначальных значений t0,t1,t2до новых значений t0+t0,t1+t1,t2+t2. Далее приращения t0,t1,t2будем рассматривать как бесконечно малые, т.е. в форме дифференциалов dt0, dt1, dt2. Исследование изменений в экономической системе при управляющем воздействии (dt0, dt1, dt2) будет проводиться в удельных показателях.

Назовем псевдоприращением (брутто-приращением) налогового бремени на одного занятого его приращение за счет приростов налоговых ставок при первоначальных удельных выпусках:

(25)

В ответ на управляющее воздействие государства dt0, dt1, dt2секторы изменяют свои удельные выпуски на dх0, dх1, dх2. Назовем базис-приращением налогового бремени (на одного занятого) его приращение за счет изменения выпусков при неизменных налоговых ставках:

(26)

Действительное приращение поступлений налогов в бюджет (на одного занятого) назовем нетто-приращением. Нетто-приращение равно сумме брутто и базис-приращений:

(27)

Точно так же нетто-приращения налоговых поступлений на одного занятого по секторам равны сумме брутто и базис-приращений:

(28)

Известно, что при квадратичной функции прибыли фирмы ее ответ на увеличение налоговой ставки однозначен: сокращение выпуска. Из приводимого ниже исследования видно, что реакция секторов сбалансированной экономики на увеличение налоговых ставок не такая однозначная. Все дело в эффекте системы: ведь рассматривается сбалансированная трехсекторная экономика, каждый сектор которой производит не столько, сколько ему захочется, а столько, каков спрос на его товар/услугу.

Условия хранения в измененном состоянии натурально-стоимостной сбалансированности трехсекторной экономики означают с математической точки зрения, что можно дифференцировать балансы (17 - 21). В результате получаем следующие пять уравнений для ds0, ds1, ds2, dp0, dp1, dp2 (для дифференциалов долей секторов в инвестициях и дифференциалов цен на их продукцию, при этом dх0, dх1, dх2являются функциями ds0, ds1, ds2) :

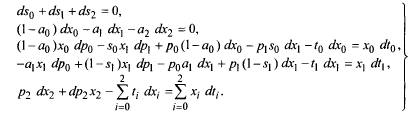(29)

Таким образом, для шести неизвестных имеется только пять уравнений. Недостающее шестое вытекает из некоторого определенного предположения о реакции секторов на изменение налоговых ставок.

В целом, возможны следующие три случая:

1. dt>0 - усиление налогового бремени;

2. dt<0 - ослабление налогового бремени;

3. dt=0 - перераспределение налогового бремени.

При сделанном предположении о неизменности ставок заработной платы наиболее реалистичной гипотезой о поведении секторов является стремление к к сохранению статус-кво, т.е. секторы пытаются так изменить свои выпуски, чтобы уровень налогообложения остался неизменным, что создает предпосылки для сохранения ставок заработной платы.

Таким образом, полную модель перераспределения налогового бремени получаем путем добавления к уравнениям (29) условия сохранения налогообложения:

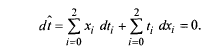(30)

Условие (30) означает, что чисто фискальные намерения государства, направленные на увеличение объема сбора налогов путем повышения налоговых ставок () могут быть изъяты соответствующими изменениями (в основном, сокращении) объемов производства: