Курсовая работа: Анализ ошибок заочной математической школы

1) понимание смысла определения (раскрытие содержания понятия).

2) понимание строения определения (родовой и видовой признаки).

3) знание условий, которым должно удовлетворять правильное определение (указываются только основные признаки, не должно быть “порочного круга”).

Ученики могут понимать определение более узко (множество объектов, подходящих под определение, меньше действительного) или более широко (множество объектов, подходящих под определение, шире действительного).

Примеры:

· по определению делимости 5 делится на 2, так как существует число 2,5 такое, что 5 = 2×2,5. Множество объектов шире действительного, так как оба множителя должны быть целыми числами.

· многие школьники четырехугольник понимают как выпуклый, понятия о существовании невыпуклого четырехугольника нет, так как в школьной практике ученики работают почти исключительно с выпуклыми фигурами. Множество объектов, удовлетворяющих определению, ýже действительного.

Ученики в рассуждениях иногда используют предложения, которые к рассматриваемому объекту применять нельзя. Например:

Задача О5: Основание призмы имеет площадь S . Ее боковое ребро длиной k наклонено к основанию под углом a. Найдите объем призмы.

Решение: Объем призмы равен произведению площади основания на длину бокового ребра, поэтому V = S × k .

Анализ ошибки: В данном случае ученик воспользовался формулой вычисления объема для прямой призмы. Для наклонной призмы эта формула не верна, следовательно, применять ее нельзя. Единственный способ искоренить ошибку – показать ученику наглядно, что его рассуждения противоречивы. Для этого возьмем прямую призму. Разделим ее на две равные части так, как показано 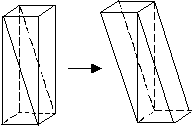на рисунке. Составим из этих частей наклонную призму. Понятно, что их объемы должны быть равны. Если же действовать подобно ученику при вычислении объемов, то объем наклонной призмы будет больше, чем объем прямой призмы.

§2. Ошибки школьников ВЗМШ и их анализ.

Эта часть основана на конкретных работах учащихся ВЗМШ. Здесь мы выделили типичные ошибки, которые допускаются школьниками при выполнении заданий по пособиям [8] – [10], входящих в программу 8 класса Кировского отделения ВЗМШ. Анализ причины и соответствующие комментарии по ее исправлению, приведенные ниже по каждой из задач, могут быть использованы проверяющими при рецензировании работ учащихся. Кроме того, анализ причин основан на классификации ошибок, которая нами уже рассмотрена в §1. На ее основе мы и будем составлять соответствующие комментарии по задачам. Номера всех задач совпадают с их номерами в пособиях [8] – [10], которые приложены к настоящей работе.

Комбинаторика. Задания №1, №2.

Задача 1-7. A È B содержит 25 элементов, A Ç B – 10 элементов, B содержит 15 элементов. Найти количество элементов в A.

Рассуждения ученика: Так как множество B содержит 15 элементов, то множество A будет содержать 25 – 15 = 10 элементов.

Анализ ошибки: Следует заметить, что, выполняя задание “Комбинаторика”, большинство учеников впервые знакомятся с теорией множеств. В связи с этим они пытаются найти свойства, схожие со свойствами уже знакомых им объектов. Так операцию объединения двух множеств школьники часто связывают с операцией сложения двух чисел. Это вполне логично, ведь в свою очередь числа еще в младшем возрасте они изучали при помощи подручных предметов, к примеру, тех же счетных палочек, то есть, фактически, с помощью операций над множествами. При решении задачи ученик действовал с множествами, как с числами. Это было бы верно, если бы пересечение множеств было пустым, как при работе со счетными палочками. Но если это не так, то число элементов в объединении и сумма количеств элементов в каждом из множеств – это разные величины. Но ученик действовал по уже сформированному стереотипу, поэтому в ответе он получил не количество элементов множества A , а количество элементов, принадлежащих только A . Исходя из классификации, данной в §1, эту ошибку следует отнести к классу необоснованных аналогий . Причина ошибки состоит в том, что ребенок при решении задачи неосознанно работает с любыми двумя множествами как с непересекающимися. Проверяющему следует помочь ученику разобраться в понятиях пересечения и объединения, сделав упор на том, что отличает объединение множеств от сложения чисел. Это можно сделать, разобрав конкретную задачу. Целесообразно использовать круги Эйлера, так как графические иллюстрации помогают ученику лучше воспринимать информацию. Рассмотрим конкретный пример.

Задача . Множество A содержит 7 элементов, множество B – 10, объединение множеств A и B – 15.Сколько элементов содержит пересечение множеств A и B (c )?

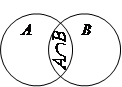Объединение множеств A и B можно разделить на три подмножества: 1) элементы, принадлежащие только множествуA ; 2) элементы, принадлежащие пересечению множеств A и B ; 3) элементы, принадлежащие только множеству B . Сложив количество элементов трех групп, мы получим количество элементов в объединении множеств A и B . Это видно и на кругах Эйлера. Обозначим за x – количество элементов пересечения. Тогда в первой группе 7 – x элементов, во второй x , в третьей 10 – x . В объединении (7 – x ) + x + (10 – x ) = 17 – x = 15 Þx = 2. Можно предложить ученику решить данную задачу в общем виде, заменив числа 7, 10 и 15 на a , b и с. Тем самым он получит выражение с = a + b – х , характеризующее количественное отношение двух множеств.

Задача 1-14. Записать формулами множества, заштрихованные на диаграммах (приведено несколько диаграмм, из которых мы рассмотрим одну).

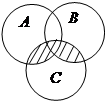Рассуждения ученика: Интересующее нас множество можно записать как A Ç C + B Ç C .

Анализ ошибки: Ученик отождествляет сложение с объединением. Надо убедить его, что между этими двумя операциями есть разница.

Не так важно, как называет ученик объединение (“объединение первого и второго множеств” или “прибавим к первому второе множество”, как-то иначе), важно то, что он подразумевает под ним, понимает ли он суть операции объединения. Поэтому нельзя считать, что ученик действовал при решении данной задачи неправильно. Надо указать, что при оперировании с числами употребляется знак “+”, а с множествами – “È”. Разделение этих операций исключает из рассуждений ненужную путаницу.

Рассуждения ученика: Интересующее нас множество можно записать формулой A Ç C + B Ç C – A Ç B Ç C .

Анализ ошибки: ученик множествами оперирует, как числами. Он решает совсем другую задачу: сколько элементов содержит заштрихованное множество. Задача проверяющего – разъяснить разницу между множеством и количеством элементов в этом множестве. Ошибка напрямую связана с формальным знанием определений операций над множествами. По классификации она относится к разделу неправильное понимание определения (неверная конкретизация). Поэтому в данной ситуации проверяющему рекомендуется дать кроме приведенных в методическом пособии определений на диаграммах, словесные определения:

AÈB – множество всех элементов, которые принадлежат либо A либо B.

AÇB – множество всех элементов, которые принадлежат и A иB одновременно.

A \ B – множество всех элементов, принадлежащих A , но не принадлежащие множеству B .

– множество всех элементов, не принадлежащих A .

Рекомендуется также сказать, что при объединении одинаковые объекты сливаются в один. Именно из таких объектов, которые содержатся в обоих множествах, и состоит пересечение. Пусть ученик сравнит определения с их графическими иллюстрациями. Сначала лучше научиться строить множества по формулам (их достаточно в пособии), а потом переходить к написанию формул по диаграммам.

Задача 2-6. Сколько существует семизначных чисел, цифры которых идут в убывающем порядке?