Курсовая работа: Анализ переходных процессов в электрических цепях

2.2 Определение переходных процессов классическим методом

В приведенной схеме (рисунок 2.1) определить классическим методом напряжения и токи переходного процесса. Построить графики переходных процессов.

2.2.1 Решение дифференциального уравнения для тока на емкости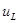

Принужденная составляющая тока на индуктивности, поэтому

2.2.2 Определение корне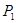й и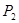

Для определения корней характеристического уравнения 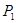и 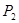составляется эквивалентная операторная схема цепи (рисунок 2.5), далее находится операторное входное сопротивление и приравнивается к нулю ().

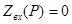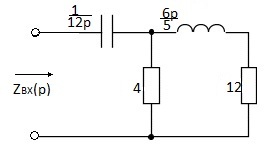
Рисунок 2.5 Эквивалентная операторная схема цепи.

Операторное сопротивление емкости , а индуктивности , тогда

Условие выполняется, если числитель равен нулю:

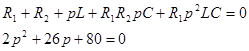
корни этого уравнения:

;

Подставим значения и в уравнение для :

2.2.3 Определение произвольных постоянных 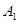и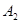

Используем значение самой функции и ее производной при , т.е. учтем начальные условия. Учитывая, что :

,

откуда получаем первое уравнение для нахождения произвольных постоянных:

Для получения второго уравнения найдем (при ) значение :

откуда получаем второе уравнение для нахождения произвольных постоянных:

Совместное решение двух уравнений

дает значения произвольных постоянных:

После подстановки произвольных постоянных в выражение для получаем: