Курсовая работа: Анализ радиосигналов и расчет характеристик оптимальных согласованных фильтров
Рекомендации по построению согласованного фильтра.
Спектральная плотность - есть коэффициент пропорциональности между длиной малого интервала частот D f и отвечающей ему комплексной амплитудой гармонического сигнала D A с частотой f0.
Спектральное представление сигналов открывает прямой путь к анализу прохождению сигналов через широкий класс радиотехнических цепей, устройств и систем.
Энергетический спектр полезен для получения различных инженерных оценок, устанавливающих реальную ширину спектра того или иного сигнала. Для количественного определения степени отличия сигнала U (t) и его смещенной во времени копии U (t- t) принято вводить АКФ.
Зафиксируем произвольный момент времени ![]() и постараемся так выбрать функцию
и постараемся так выбрать функцию ![]() , чтобы величина
, чтобы величина ![]() достигала максимально возможного значения. Если такая функция действительно существует, то отвечающий ей линейный фильтр называют согласованным фильтром.
достигала максимально возможного значения. Если такая функция действительно существует, то отвечающий ей линейный фильтр называют согласованным фильтром.
Введение
Курсовая работа по заключительной части предмета "Теория радиотехнических сигналов и цепей" охватывает разделы курса, посвященного основам теории сигналов и их оптимальной линейной фильтрации.
Целями работы являются:
изучение временных и спектральных характеристик импульсных радиосигналов, применяемых в радиолокации, радионавигации, радио телеметрии и смежных областях;
приобретение навыков по расчету и анализу корреляционных и спектральных характеристик детерминированных сигналов (автокорреляционных функций, спектров амплитуд и энергетических спектров).
В курсовой работе для заданного типа сигнала необходимо произвести:
Расчет АКФ.
Расчет спектра амплитуд и энергетического спектра.
Импульсной характеристики согласованного фильтра.
В данной курсовой работе рассматривается прямоугольная когерентная пачка трапецеидальных радиоимпульсов.
Параметры сигнала:
несущая частота (частота радиозаполнения),1,11 МГц
длительность импульсов, (длительность основания) 15 мкс
частота следования,11,2 кГц
число импульсов в пачке,9
Автокорреляционная функция (АКФ) сигнала U (t) служит для количественного определения степени отличия сигнала U (t) и его смещённой во времени копии 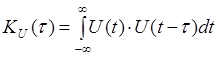 (0.1) и при t = 0 АКФ становится равной энергии сигнала. АКФ обладает простейшими свойствами:
(0.1) и при t = 0 АКФ становится равной энергии сигнала. АКФ обладает простейшими свойствами:
свойство чётности:
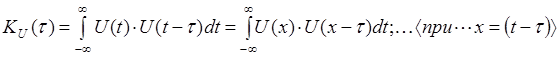 т.е. K U (t ) =K U (- t ).
т.е. K U (t ) =K U (- t ).
при любом значении временного сдвига t модуль АКФ не превосходитэнергии сигнала: ½K U (t ) ½£K U (0 ), что вытекает из неравенства Коши - Буняковского.
Итак, АКФ представляется симметричной кривой с центральным максимумом, который всегда положителен, а в нашем случае АКФ имеет ещё и колебательный характер. Необходимо отметить, что АКФ имеет связь с энергетическим спектром сигнала: 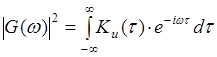 ; (0.2) где ½G (w ) ½
; (0.2) где ½G (w ) ½![]() квадрат модуля спектральной плотности. Поэтому можно оценивать корреляционные свойства сигналов, исходя из распределения их энергии по спектру. Чем шире полоса частот сигнала, тем уже основной лепесток автокорреляционной функции и тем совершеннее сигнал с точки зрения возможности точного измерения момента его начала.
квадрат модуля спектральной плотности. Поэтому можно оценивать корреляционные свойства сигналов, исходя из распределения их энергии по спектру. Чем шире полоса частот сигнала, тем уже основной лепесток автокорреляционной функции и тем совершеннее сигнал с точки зрения возможности точного измерения момента его начала.
Часто удобнее вначале получить автокорреляционую функцию, а затем, используя преобразование Фурье, найти энергетический спектр сигнала. Энергетический спектр - представляет собой зависимость ½G (w ) ½![]() от частоты.
от частоты.
Согласованные же с сигналом фильтры обладают следующими свойствами:
Сигнал на выходе согласованного фильтра и функция корреляции выходного шума имеют вид автокорреляционной функции полезного входного сигнала.
Среди всех линейных фильтров согласованный фильтр даёт на выходе максимальное отношение пикового значения сигнала к среднеквадратичному значению шума.