Курсовая работа: Анализ радиосигналов и расчет характеристик оптимальных согласованных фильтров

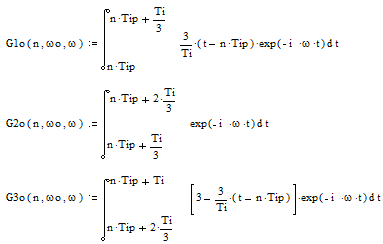
и преобразованием Фурье для получения спектральных функций, которые с учётом пределов интегрирования для n-го импульса будут рассчитываться по формулам:

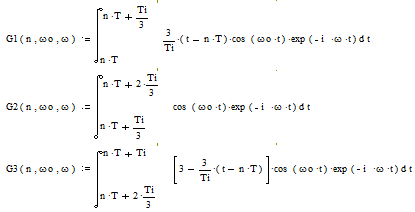
для огибающей радиоимпульса и:

для радиоимпульса соответственно.

Далее вычисляем спектральную плотность огибающей радиосигнала для всех N импульсов в соответствии с выражением:

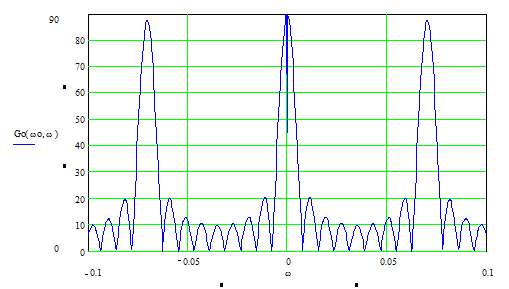
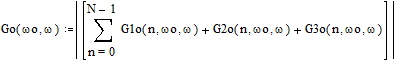
График этой функции представлен на (рис.5).

на рисунке для наглядности рассмотрен разный частотный диапазон

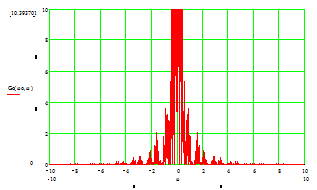
Рис. 6. Спектральная плотность огибающей радиосигнала.

Как и ожидалось, главный максимум расположен в центре, т.е. при частоте w =0.

Энергетический же спектр равен квадрату спектральной плотности и поэтому график спектра имеет вид как на (рис 6) т.е. очень похож на график спектральной плотности:

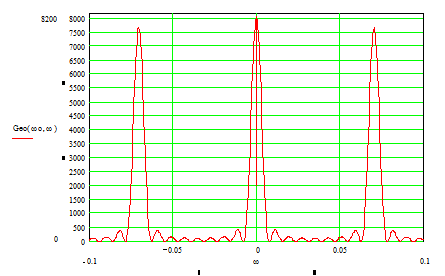
Рис. 7. Энергетический спектр огибающей радиосигнала.

Вид спектральной плотности для радиосигнала будет иной, поскольку вместо одного максимума при w = 0 будет наблюдаться два максимума при w = ±wо, т.е. спектр видеоимпульса (огибающей радиосигнала) переносится в область высоких частот с уменьшением вдвое абсолютного значения максимумов (см. рис.7). Вид энергетического же спектра радиосигнала будет так же очень похож на вид спектральной плотности радиосигнала, т.е. тоже будет осуществлён перенос спектра в область высоких частот и так же будет наблюдаться два максимума (см. рис.8).

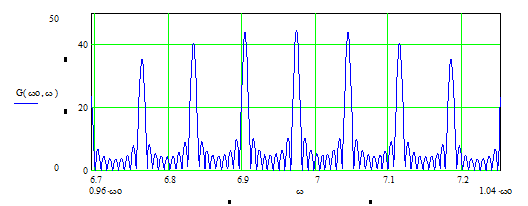
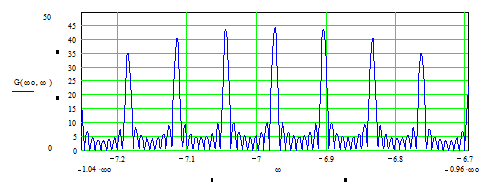
Рис. 8. Спектральная плотность пачки радиоимпульсов.

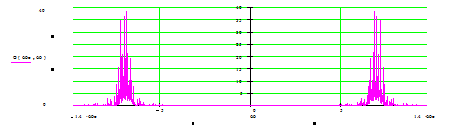
Рис. 9.

Расчёт импульсной реакции и рекомендации к построению согласованного фильтра

Как известно, наряду с полезным сигналом, зачастую присутствуют шумы и поэтому при слабом полезном сигнале иногда трудно определить есть полезный сигнал или нет.

Для приёма сигнала сдвинутого во времени на фоне белого гауссовского шума (белый гауссовский шум "БГС" имеет равномерную плотность распределения) n (t) т.е. y (t) = + n (t), отношение правдоподобия при приёме сигнала известной формы имеет вид:

где No - спектральная плотность шума.

Поэтому приходим к выводу, что оптимальная обработка принимаемых данных - суть корреляционный интеграл

Полученная функция представляет собой ту существенную операцию, которую следует выполнить над наблюдаемым сигналом с тем, чтобы оптимальным (с позиции критерия минимума среднего риска) образом принять решение о наличии или отсутствии полезного сигнала.