Курсовая работа: Анализ радиосигналов и расчет характеристик оптимальных согласованных фильтров

Рис.1. Прямоугольная когерентная пачка трапецеидальных радиоимпульсов

В нашем случае сигнал представляет собой прямоугольную пачку трапецеидальных (длительность вершины равна одной третьей длительности основания) радиоимпульсов (см. рис 1) в которой число импульсов N=9, а длительность импульса T_i =15 мкс.

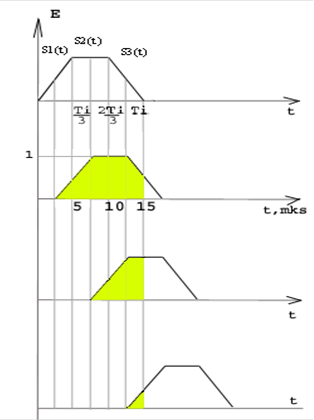
Рис.2. Сдвиг копии огибающей сигнала

S3(t)

S2(t)

S1(t)

?????? ?????????? ????????? ? ????? T_ip ? 89,286 ???., ??????? ?????????? q = T_ip /T_i = 5,952. ??? ??????? ??? ????????????? ???????? (0.1) ? ??????????? ?????????????? ????????? ?? ??????? ????? ??????? ?? ??????? ?????? ???????????????? ???????? (?????????). ??? ????? ????????? ? рисунку 2. ??? ??????? ???????? ???????? ??? ????????? ??????? (????????) ?????????? ??? ??????????:

Для величины сдвига T принадлежащего промежутку от нуля до одной третьей длительности импульса необходимо решить интеграл:

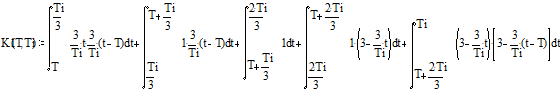
Решая этот интеграл, получаем выражение для главного лепестка АКФ данного сдвига копии огибающей сигнала:

Для T принадлежащего промежутку от одной третьей до двух третьих длительности импульса получаем следующий интеграл:

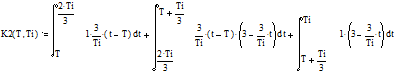
Решая его, получаем:

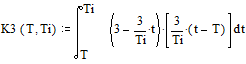
Для Т, принадлежащего промежутку от двух третьих длительности импульса до длительности импульса интеграл, имеет вид:

Поэтому в результате решения имеем:

С учётом свойства симметрии (чётности) АКФ (смотрите введение) и соотношения, связывающего АКФ радиосигнала и АКФ его комплексной огибающей: имеем функции для главного лепестка АКФ огибающей ko (T) радиоимпульса и АКФ радиоимпульса Ks (T):

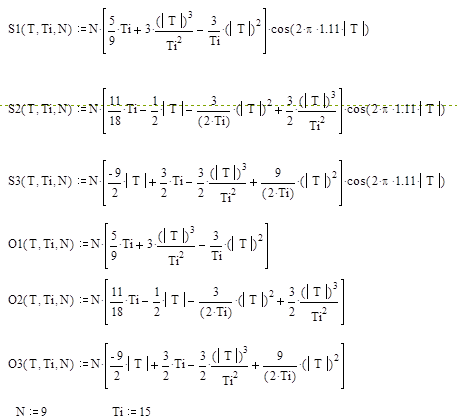
в которых, входящие функции, имеют вид:

Таким образом, на рисунке 3 изображён главный лепесток АКФ радиоимпульса и его огибающей, т.е. когда в результате сдвига копии сигнала, когда участвуют все 9 импульсов пачки, т.е. N = 9.

Видно, что АКФ радиоимпульса имеет колебательный характер, но в центре обязательно максимум. При дальнейшем сдвиге число пересекающихся импульсов сигнала и его копии будет уменьшаться на единицу, а, следовательно, и амплитуда через каждый период следования T_ip = 89,286 мкс.

Поэтому, окончательно АКФ будут иметь вид как на рисунке 4 ( 16 лепестков, отличающихся от главного только амплитудами) с учётом того, что на этом рисунке Т=T_{ip .:}

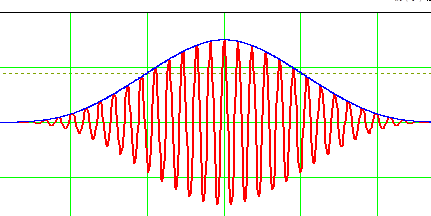
Рис. 3. АКФ главного лепестка радиоимпульса и его огибающей

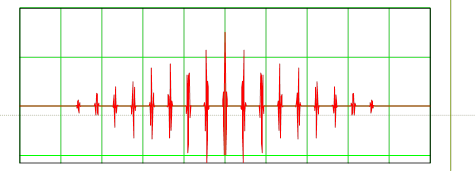
Рис. 4. АКФ Прямоугольной когерентной пачки трапецеидальных радиоимпульсов

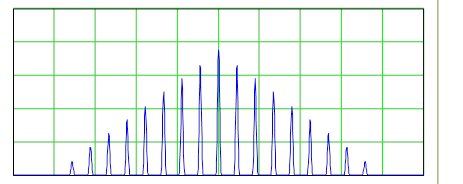
Рис. 5. Огибающая пачки радиоимпульсов.

Расчёт спектральной плотности и энергетического спектра