Курсовая работа: Аналіз теоретичної бази інтерполювання функції

Таблиця 2- Таблиця різниць функції

2	-4.58579
-11.68216
3	-16.26795	-6.04989
-17.73205	0.01801
4	-34	-6.03188	-0.00878
-23.76393	0.00923	0.00504
5	-57.76393	-6.02265	-0.00374	-0.00321
-29.78658	0.00549	0.00183	0.00218
6	-87.55051	-6.01716	-0.00191	-0.00103	-0.00287
-35.80374	0.00358	0.0008	0.00069
7	-123.35425	-6.01358	-0.00111	-0.00034
-41.81732	0.00247	0.00046
8	-165.17157	-6.01111	-0.00065
-47.82843	0.00182
9	-213	-6.00929
-53.83772
10	-266.83772

Розв’язок:

Приймемо і , тоді

.

Оскільки , то скористаємося формулою Бесселя. Маємо:

;

Звідси, використовуючи підкреслені різниці, отримаєм:

2. Розробка алгоритмів та вибір оптимального алгоритму

При розробці алгоритму обчислення значення функції за допомогою інтерполяційної формули Бесселя будемо використовувати формулу яка описана в теоретичних відомостях.

Аналіз формули та прикладу, наведеного в першому розділі, показує що для обчислення значення функції необхідно обчислити значеня кінцевих різниць а також значеннь q та р. Безпосереднє обчислення за формулою вимагає 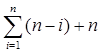операцій додавання (віднімання), n - операцій ділення та 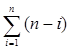- операцій множення. З врахуванням того, що час виконання операції множення та ділення відповідно в 1,14 та 2,33 рази більший за час виконання операції додавання (віднімання) при використанні математичного співпроцесора, загальна кількість операцій обчислення складає

Алгоритм можна побудувати таким чином, щоб спочатку обчислити всі всі знаменники поліному, а потім провести обчислення за основною формулою. В цьому випадку необхідно 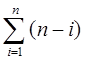комірок пам’яті.

Інший спосіб побудови алгоритму полягає в тому, щоб проводити обчислення знаменників поліному одночасно з обчисленнями за основною формулою виходячи з факторіалу. В цьому випадку для збереження значень необхідно лише n-1 комірок пам’яті.

Комплексний коефіцієнт ефективності Ке одного алгоритму в порівнянні з іншим можна обчислити за формулою

де Кч – коефіцієнт ефективності за часом виконання;

Кn – коефіцієнт ефективності за затратами пам’яті алгоритму.

Оскільки коефіцієнт ефективності за часом виконання алгоритму можна приблизно оцінити за кількістю арифметичних операцій алгоритму, то комплексний коефіцієнт ефективності описаних вище алгоритмів складає

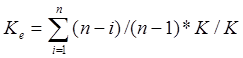
Для випадку коли n=9

Блок-схеми описаних вище алгоритмів відповідно на рис 2.1 та рис 2.2. В даних алгоритмах вважається, що матриця A використовуються для збереження таблиці різниць, значення x, x0, n, q – однойменні змінні [6].

3 . Приклад програми обчислення значення функції за допомогою інтерполяційної формули Бесселя

3.1 Інструкція користувача

Після виклику Pascal ABC із середовища Windows на екрані з'являється командне вікно середовища Pascal ABC.

Це вікно є основним у Pascal ABC. У ньому відображаються символи команд, що набираються користувачем на клавіатурі, результати виконання цих команд, текст програми, що виконується, а також інформація про помилки виконання програми, яка розпізнана системою.

Ознакою того, що програма Pascal ABC готова до сприйняття і виконання чергової команди, є наявність в останньому рядку текстового поля вікна миготливої вертикальної риски.

У верхній частині командного вікна (безпосередньо під заголовком Pascal ABC) розташований рядок меню, що складається з шести меню –Файл, Правка, Вид, Программа, Сервис, Помощь. Під головним меню розміщена панель інструментів з піктограмами, що дозволяють виконувати деякі найбільше часто використовувані операції.