Курсовая работа: Анализ зависимости между уровня комплемента в крови больных системной красной волчанкой и степен

R₁ =

57877

R₂ =

23298.5

R₃ =

21259.5

R₄ =

8789

R₅ =

3072

N = 479	k = 5
R1 = 57877	n1 = 210
R2 = 23298,5	n2 = 101
R3 = 21259,5	n3 = 98
R4 = 8789	n4 = 45
R5 = 3072	n5 = 25

Теперь можно полученные суммы рангов подставить в формулу и получить значение критериальной статистики Краскела-Уоллиса [4] :

Н=23,03

Полученный результат не является незначимым, поэтому нельзя считать, что выборки извлечены из одинаково распределенных совокупностей и что средние значения совокупностей совпадают. Но этот вывод является приближенным, так как в нашей таблице есть много совпадающих значений. Для учета влияния связей можно воспользоваться модифицированной формой статистики Краскела-Уоллиса [4]:

Н^` =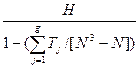

, где g – число групп совпадающих значений, Т_j = (t - t), t– число совпадающих наблюдений в группе с номером j .

Таблица №4. Группы совпадающих наблюдений.

Повторяющиеся значения УК	Кол-во повторений tj	Значение Tj
0	25	15600
5	4	60
6	2	6
10	9	720
11	3	24
12	5	120
13,6	2	6
15	6	210
15,6	2	6
16	5	120
18	4	60
19,5	3	24
20	11	1320
21	2	6
22	2	6
22,4	2	6
22,5	4	60
23	3	24
24	5	120
24,5	2	6
25	10	990
25,1	2	6
26,1	2	6
26,5	2	6
27	6	210
28	4	60
28,7	2	6
28,9	4	60
29	3	24
29,4	2	6
30	6	210
30,4	2	6
30,8	2	6
31	4	60
32	8	504
32,3	3	24
32,6	2	6
33	17	4896
33,3	3	24
33,5	7	336
34	2	6
34,1	3	24
34,3	3	24
34,4	2	6
34,7	2	6
35	13	2184
35,5	2	6
35,6	3	24
35,8	2	6
36	5	120
36,6	3	24
36,9	3	24
37	4	60
37,3	2	6
37,4	2	6
37,7	2	6
37,9	2	6
38	10	990
38,2	3	24
38,5	3	24
38,6	2	6
39	3	24
39,1	3	24
39,2	3	24
39,3	2	6
40	12	1716
40,3	2	6
40,4	2	6
41	3	24
41,7	3	24
42	4	60
43	7	336
43,5	2	6
43,8	4	60
44	2	6
45	12	1716
45,7	2	6
46	6	210
46,7	2	6
47	2	6
47,5	2	6
48	4	60
48,2	2	6
49,1	3	24
50	14	2730
51	2	6
52,2	2	6
60	3	24

g = 88

Теперь можно полученные результаты подставить в модифицированную формулу и получить уточненное значение критериальной статистики Краскела-Уоллиса :

Н^` = 23,037

Вывод. Скорректированное значение Н^` статистики Краскела-Уоллиса несущественно отличается от значения Н, т.о. мы можем отвергнуть гипотезу Н₀ на минимальном уровне значимости. Следовательно , мы подтвердили результат полученный ранее : существует зависимость между УК в крови больных СКВ и степенью тяжести поражения почек .

3. Непараметрический дисперсионный анализ по одному признаку с применением критерия Джонкхиера для нескольких выборок, упорядоченных по возрастанию влияния фактора

Нам заранее известно, что имеющиеся группы результатов упорядочены по возрастанию влияния фактора.. В нашем случае фактором является степень тяжести ГН. В таких случаях целесообразно использовать критерий Джонхиера , более чувствительный против альтернатив об упорядоченном влиянии фактора [5].

Статистическая модель

Имеется k совокупностей, в нашем случае 5 совокупностей. Каждая выборка извлекается из своей совокупности. Все наблюдения независимы. имеющиеся группы результатов упорядочены по возрастанию влияния фактора . 1-й столбец Таблицы №1 отвечает наименьшему уровню фактора, последний – наибольшему, а промежуточные столбцы получили номера, соответствующие их положению. В нашем случае фактором является степень тяжести поражения почек [4] .

Гипотезы

Н₀ :==…= ( влияние фактора упорядоченно.)

Н₁ : …

Критическая область

Верхняя 5% область F-распределения, что в нашем случае соответствует значению критерия, превышающему значение 2,21. Данное число взято из таблицы А.4 на стр. 334 [6].