Курсовая работа: Базисные сплайны

Так как для разделенной разности порядка от функции по точкамсправедливо равенство

Если использовать тождество то можно получить несколько иную форму записи этой функции

Из определения усеченных степенных функций следует, что функцияявляется сплайном степени п дефекта 1 на

сетке узлов

Лемма 1.1. Справедливо тождество

Доказательство. Еслито разделенная разность функции по точкам может быть вычислена по формуле Лейбница:

Для разности порядка путем рассуждений по индукции нетрудно получить

Представим функциюв виде

и построим ее разделенную разность порядка по формуле Лейбница. Получим

Отсюда, если учесть определение сплайнов, следует тождество (4).

Лемма 1.2. Сплайны обладают следующими свойствами:

Доказательство. Функцияравна нулю при и является многочленом степени n от х при . Поэтому ее разделенные разности порядка по значениям аргументатождественно равны нулю при и т.е. Внутри интервала

В самом деле, при n = 0 согласно (2) . Пусть, далее, утверждение а) верно при Тогда при n = l в силу (4) на интервале функцияявляется линейной комбинацией с положительными весами функцийпричем по предположению в произвольной точке указанного интервала хотя бы одна из этих функций больше нуля. Следовательно, для , и утверждение а) установлено.

Докажем утверждение б). Всякую n+1 раз непрерывно дифференцируемую функцию g(t) на промежутке а ≤ t ≤ b можно представить формулой Тейлора с остаточным членом в интегральной форме:

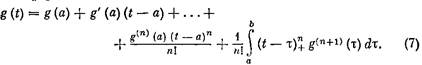
Здесь под знаком интеграла вместо обычного сомножителя стоит усеченная степенная функция, что позволяет заменить переменный верхний предел t постоянной величиной b. Из (7) следует разностное соотношение

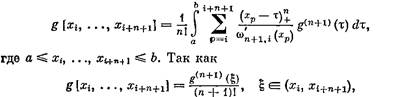
то, полагая g(x) = x^{n +1} , поручаем