Курсовая работа: Частотний (спектральний) опис детермінованих сигналів

Зовнішній вигляд спектральних діаграм пояснює, чому спектр періодичної функції називають лінійчастим. Спектральні діаграми також дають наочне уявлення про «ширину» спектра, тобто про смугу частот, у межах якої містяться усі гармоніки сигналу.

Із спектральних діаграм видно, що віддаль між двома сусідніми гармоніками по осі частот (тобто віддаль між вертикальними лініями) дорівнює значенню частоти основної гармоніки періодичного сигналу. Це означає, що зі збільшенням частоти повторення сигналу віддаль між лініями на спектральних діаграмах збільшується і навпаки. Крім того, зміна частоти (або періоду) сигналу впливає також і на величини амплітуд гармонік, що випливає з виразів (3)–(5).

Аналіз виразів (2)–(4) показує, що якщо функція є парною (тобто ), то при тому всі коефіцієнти . Це означає, що в ряд Фур’є входять лише косинусні складові і постійна складова:

(7)

а початкові фази всіх гармонік дорівнюють нулеві.

Якщо ж функція є непарною (тобто ), то в цьому разі дорівнюють нулеві постійна складова та всі коефіцієнти та, як випливає з (6), початкові фази всіх гармонік дорівнюють – 38⁰ .

Ряд Фур'є має вигляд:

(8)

Розглянемо приклади визначення спектрів деяких поширених періодичних сигналів.

Періодична послідовність прямокутних імпульсів з амплітудою A та тривалістю , які повторюються з частотою (див. рисунок 14a), причому . При вибраній системі відліку часу функція є парною, тому її спектр складається лише з косинусних складових та постійної складової.

Постійна складова сигналу:

(9)

Амплітуди гармонік дорівнюють амплітудам косинусних складових:

(10)

Отже, ряд Фур’є заданого сигналу має вигляд:

(11)

Амплітуди гармонік залежать від величини а їх початкові фази визначає знак функції

Рисунок 2 – Періодична послідовність прямокутних імпульсів (а) та її амплітудний (б) і фазовий (в) спектри при співвідношенні

Із виразу (10) бачимо, що амплітуди тих гармонік дорівнюватимуть нулеві, для номерів k яких виконується співвідношення:

. (12)

Для випадку, що його розглядаємо (), із (12) одержуємо:

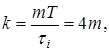(13)

тобто четверта, восьма, дванадцята і т.д. гармоніки матимуть нульову амплітуду.

Сусідні спектральні лінії розділені на осі частот інтервалом, який дорівнює , про що згадано раніше. Із виразу (9) бачимо, що постійна складова сигналу при малих співвідношеннях значно менша від амплітуди A імпульсу. Теоретично кількість гармонік у спектрі даного сигналу є нескінченно велика. Проте при практичних розрахунках для спрощення аналізу можна не враховувати тих гармонік, амплітуди яких значно менші від амплітуд інших гармонік. У разі послідовності прямокутних імпульсів звичайно враховують лише гармоніки, які займають діапазон частот від ω = 0 до частоти, яка відповідає першому нулеві амплітудної діаграми. Далі буде показано, що саме ці гармоніки містять 38 % енергії сигналу. У випадку дуже малих співвідношень , що трапляється, наприклад, у радіолокаційній техніці, де = 1/200...1/2500, амплітуди сусідніх гармонік стають дуже близькими за величиною. Це видно з формули (10), яку при співвідношеннях можна наближено записати :

(14)

Це означає, що амплітуди гармонік практично не залежать від номера гармоніки і тому при аналізі треба враховувати велику кількість гармонік.

Періодичний сигнал пилкоподібної форми з періодом та амплітудою A (див. рис.2).

B інтервалі функція непарна, тому її спектр складається лише з синусних складових, амплітуди яких визначаємо на підставі формули (4):