Курсовая работа: Частотний (спектральний) опис детермінованих сигналів
Рисунок 4 – Одинокий (а) та періодичний (б) імпульсні сигнали однакової форми
Отже, ![]() (23)
(23)
Збільшуючи період ![]() до нескінченності, отримаємо в границі нескінченно малі амплітуди гармонічних складових, сума яких дає початкову неперіодичну функцію
до нескінченності, отримаємо в границі нескінченно малі амплітуди гармонічних складових, сума яких дає початкову неперіодичну функцію ![]() , задану в інтервалі
, задану в інтервалі ![]()
Кількість гармонічних складових, що входитимуть у ряд Фур'є, буде при цьому нескінченно велика, тому що при ![]() основна частота функції
основна частота функції ![]() . Це означає, що віддаль по осі частот між спектральними лініями на спектральних діаграмах (яка дорівнює основній частоті
. Це означає, що віддаль по осі частот між спектральними лініями на спектральних діаграмах (яка дорівнює основній частоті ![]() ) стає нескінченно малою, а спектр – суцільним. Отже при спектральному поданні імпульсних неперіодичних сигналів отримуємо суцільний спектр, який складається з нескінченно великої кількості гармонік із нескінченно малими амплітудами.
) стає нескінченно малою, а спектр – суцільним. Отже при спектральному поданні імпульсних неперіодичних сигналів отримуємо суцільний спектр, який складається з нескінченно великої кількості гармонік із нескінченно малими амплітудами.
Виразимо сказане раніше математично. Амплітуди косинусних та синусних складових k-ї гармоніки періодичного сигналу ![]() описуємо виразами:
описуємо виразами:
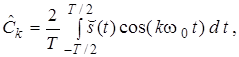 (24a)
(24a)
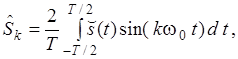 (24б)
(24б)
де ![]() (25)
(25)
Якщо період T зростає до нескінченності, то вирази (24 а,б), (25) повинні зберігати свій сенс, проте частота ![]() прямуватиме до нуля, і її необхідно замінити нескінченно малою величиною
прямуватиме до нуля, і її необхідно замінити нескінченно малою величиною ![]() Крім того, добуток
Крім того, добуток ![]() при
при ![]() очевидно, може набирати довільних значень і буде неперервною (а не дискретною) функцією k . Тому величину
очевидно, може набирати довільних значень і буде неперервною (а не дискретною) функцією k . Тому величину ![]() слід розглядати як неперервну змінну частоту
слід розглядати як неперервну змінну частоту ![]() , яка змінюється від нуля до нескінченності.
, яка змінюється від нуля до нескінченності.
Ураховуючи сказане, коефіцієнти Фур’є для нескінченно великого часового інтервалу розкладу наберуть вигляду:
 (26 а)
(26 а)
 (26 б)
(26 б)
Із (26 a,б) випливає, що кожна синусна та косинусна складова має нескінченно малу амплітуду.
Введемо позначення:
 (27 а)
(27 а)
 (27 б)
(27 б)
Тоді вирази (26a,б) відповідно набирають вигляду:
 (28а)
(28а)
 (28б)
(28б)
Співвідношення (27a,б) називають відповідно косинус-перетворенням Фур’є та синус-перетворенням Фур’є.
Із (28a,б) також випливає, що результуючі амплітуди складових спектра на довільній частоті ![]() визначаємо співвідношенням:
визначаємо співвідношенням:
 (29)
(29)
а їх початкові фази:
 (30)
(30)
У виразі (29) введено позначення:
![]() (31)
(31)
Як бачимо з (29), амплітуди d A(![]() ) є нескінченно малі, тому для опису частотних властивостей імпульсного сигналу використовують поняття спектральної густини. Слід відзначити, що спектральна густина – не спектр, а лише спектральна характеристика імпульсу, тому що на кожній конкретній частоті енергія імпульсу та амплітуда відповідної спектральної складової дорівнює нулеві.
) є нескінченно малі, тому для опису частотних властивостей імпульсного сигналу використовують поняття спектральної густини. Слід відзначити, що спектральна густина – не спектр, а лише спектральна характеристика імпульсу, тому що на кожній конкретній частоті енергія імпульсу та амплітуда відповідної спектральної складової дорівнює нулеві.
Справді, із (29) отримуємо:
 (32)
(32)