Курсовая работа: Частотний (спектральний) опис детермінованих сигналів

Ряд Фур'є даного коливання має вигляд:

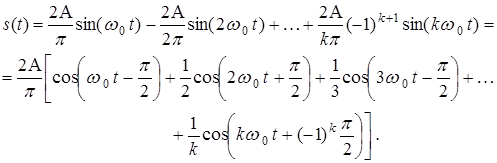(16)

Із (15) видно, що амплітуди гармонік зменшуються прямопропорційно номерові k гармоніки, початкові фази всіх непарних гармонік дорівнюють – 38°, а парних гармонік + 38°.

2 Комплексна форма опису ряду Фур ’ є

Поряд із тригонометричною формою запису ряду Фур'є часто використовують компактнішу комплексну форму, до якої можна перейти від (1 а,б), використавши формулу Ейлера:

. (17)

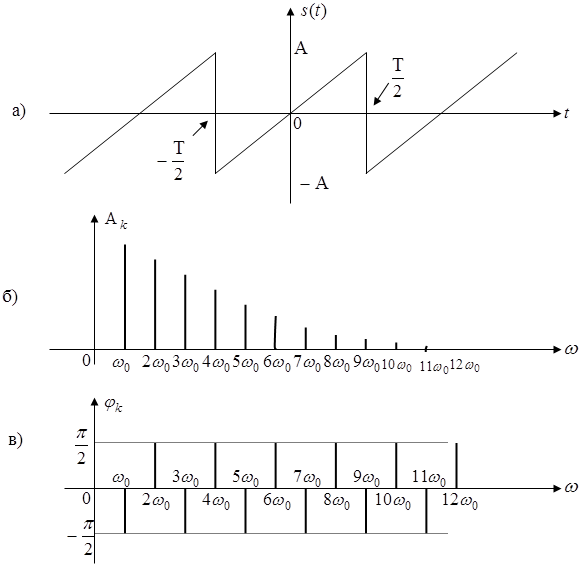
Рисунок 3 – Періодичний сигнал пилкоподібної форми (а) та його амплітудний (б) і фазовий (в) спектри

Справді, з урахуванням (17) записуємо:

(18)

Величину

(19)

прийнято називати комплексною амплітудою k -ої гармоніки. Вона несе інформацію про амплітуду та початкову фазу даної гармоніки.

Величину: називають комплексно спряженою з величиною.

Тепер вирази (1a,б) можна записати так:

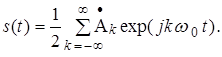(20)

Отриманий вираз є комплексною формою запису ряду Фур’є. У виразі (20) додавання ведеться як за додатними, так і за від’ємними значеннями k . Це означає, що в комплексний ряд Фур’є входять гармоніки з додатними і від’ємними частотами. Від’ємні частоти не мають фізичного сенсу. Вони з’являються як результат формального подання дійсної функції часу з допомогою комплексної форми.

Комплексні амплітуди можна визначити на підставі функції за формулою:

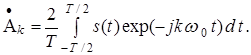(21)

Ha підставі (21) знаходимо взаємозв'язок між величинами та C_k і S_k , які описуємо виразами (3), (4):

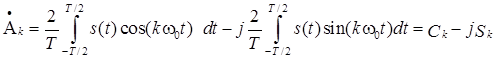. (22)

Зауважимо, що для від’ємних значень Для де A₀ визначаємо виразом (2).

Формули (20) та (21) називають парою перетворень Фур’є. Перша формула дає змогу визначити сигнал, якщо відомий його спектр, друга – визначити спектр сигналу, якщо задана функція , яка описує сигнал.

3 Спектральний опис імпульсних сигналів

Приймемо, що заданий сигнал має форму одинокого імпульсу (див. рис. (16а), який відрізняється від нуля на інтервалі .

Крім того, функція задовольняє умови Діріхле в будь-якому скінченному інтервалі і є абсолютно інтегрованою, тобто

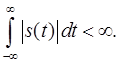
Для проведення спектрального аналізу даного сигналу вчинимо так: перетворимо задану неперіодичну функцію у періодичну повторенням її з довільним періодом (рис. 16б). Отриману періодичну функцію можна розкласти в ряд Фур’є, причому коефіцієнти ряду Фур’є будуть тим менші, чим більший буде вибрано інтервал як період. Це випливає з виразів (2)–(4). Якщо період збільшувати до нескінченності, то всі імпульси, крім первинного, відсунуться у нескінченність і залишиться лише первинний імпульс .