Курсовая работа: Частотно-избирательные фильтры Фильтр нижних частот Чебышева

Амплитудно-частотная характеристика оптимального фильтра нижних частот удовлетворяет обозначенным на рис. 1.5.1 (или на рис. 1.5.2) условиям для данного порядка п и допустимого отклонения в полосах пропускания и задерживания при минимальной ширине переходной области. Таким образом, если заданы значения A, A₁ , А₂ , nи w_c , то значение частоты w₁ минимально. Для полиномиальной характеристики оптимальной является характеристика фильтра Чебышева. Однако в общем случае оптимальным является эллиптический фильтр, характеристики которого значительно лучше характеристик фильтра Чебышева.

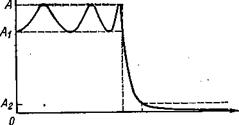
Рис. 1.5.3. Амплитудно-частотная характеристика фильтра Чебышева шестого порядка

Рис. 1.5.4. Амплитудно-частотная характеристика инверсного фильтра Чебышева шестого порядка

1.6 Фильтры нижних частот на ИНУН

Схема на ИНУН, реализующая функцию фильтра нижних частот Баттерворта или Чебышева второго порядка вида

изображена на рис. 1.6. Анализируя эту схему, получаем:

;

; (1.4)

.

Значения сопротивлений определяются следующим образом:

;

;

; (1.5)

.

где С₂ имеет предпочтительно близкое к значению 10/f_с мкФ.

А С₁ должно удовлетворять следующему неравенству

Рис. 1.6. Схема фильтра нижних частот на ИНУН

1.7 Расчет фильтра нижних частот на Инун

Для расчета фильтра нижних частот или Чебышева более высокого порядка, обладающего заданной частотой среза f_с (Гц), или w_с =2πf_с и коэффициентом усиления К = 1, необходимо выполнить следующие шаги.

1. Найти нормированные значения коэффициентов нижних частот В и С из соответствующей таблицы в приложении А.

2. Выбрать номинальное значение емкости С₂ (предпочтительно близкое к значению 10/fмкФ) и вычислить значения сопротивлений по (1.5)

3. Выбрать номинальные значения, наиболее близкие к вычисленным значениям, и реализовать фильтр или его звенья в соответствии со схемой, показанной на рис. 1.6.

2. Техническое задание

1. Фильтр Чебышева верхних частот на ИНУН;