Курсовая работа: Частотно-временной анализ сигналов

, (3.5.3)

где константы А и В такие, что . Условие (3.5.3.) в терминах радиотехники имеет довольно прозрачное толкование. Действительно, так как при каждом значении масштаба вейвлет представляет собой полосовой фильтр, то набор (сумма) этих фильтров (блок фильтров) является некоторым устройством с неравномерной частотной характеристикой, определяемой константами A и B (рис. 3.12). Сигнал, например звуковой, на выходе такого устройства при сильной неравномерности частотной характеристики претерпевает существенные искажения. Поэтому для его восстановления принимают специальные меры, в частности, устанавливают фильтр, компенсирующий искажения частотной характеристики. В вейвлет-преобразовании таким фильтром является дуальный (или двойственный) вейвлет , Фурье-образ которого имеет вид:

. (3.5.4.).

Покажем, что с помощью такого вейвлета по коэффициентам DWT полностью восстанавливается сигнал. Действительно, используя соотношение Парсеваля

()

и формулу получим (3.5.4.):

Из (3.5.4.) и (3.5.3.) можно показать, что

4.2 Дискретизация масштаба и сдвига. Фреймы

В этом случае полагают дискретными величины a и b, т.е. Частотное окно для анализа сохраняется прежним. Ширина временного окна

равна , а среднее значение изменяется дискретно пропорционально m -ой степени a₀ - масштабу вейвлета. Чем уже функция ψ, т.е. меньше величина, тем меньше (на ту же величину) шаг сдвига этой функции. Базисными функциями для дискретного вейвлет-преобразования будут функции, получаемые из ,при и

Коэффициенты разложения любой функции из L₂ могут быть получены как

Выражение (3.5.6) является дискретным вейвлет-преобразованием функции . Чтобы обратное преобразование во временную область было справедливым, должно выполняться следующее условие:

для всехесли константы A и B такие, чтоВ этом случае формула для восстановления функции f(t) по коэффициентам будет иметь вид

(3.5.8)

где ошибку восстановления R можно оценить как Разделив все члены неравенства (3.5.7) на, можно видеть, что константы A и B являются границами нормированной наэнергии – скалярного произведения. Они (эти константы) как бы "обрамляют" нормированную энергию коэффициентов Отсюда произошел термин фрейм (frame), которым называют множество функций при которых условие (3.5.7) выполняется. Если A= B , то и множество называют плотным фреймом. При этом выражение вытекающее из (3.5.7), является обобщением теоремы Парсеваля на плотные фреймы. Для плотных фреймов из (3.5.8) получаем

Если A=B=1, то плотный фрейм становится ортогональным базисом. Заметим, что для вейвлетов, образованных материнским вейвлетом (3.3.6), хорошие результаты при восстановлении сигналов получаются при так как . Для больших величин, например будет т.е. восстановление приводит к большим искажениям.

4.3 Примеры вейвлетов для дискретного преобразования

Как было отмечено выше, функции вейвлет обладают свойством частотно-временной локализации, т.е. они ограничены как в частотной, так и во временной областях. Ниже рассмотрим два примера: первый – спектр вейвлетов в частотной области представляет собой идеальный полосовой фильтр, второй – сами функции вейвлет представляют собой прямоугольники. Все вейвлеты, с точки зрения частотно-временных свойств, занимают промежуточное положение между этими крайними случаями.

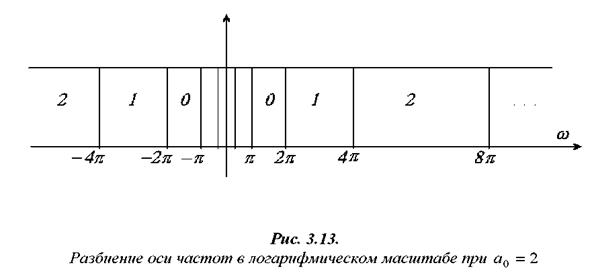
Sinc-базис. Разобьем ось частот на интервалы (поддиапазоны), как показано на рис. 3.13 при a₀ = 2. Такое разбиение называют логарифмическим, так как отношение верхней и нижней границ диапазонов постоянно и равно 2. Такое разбиение является еще и идеальным, так как оно реализуется идеальными полосовыми фильтрами. Подобная идеализация нужна для исследования свойств частотного разложения с помощью идеализированных вейвлетов, что позволит в дальнейшем перейти к более сложным разложениям. Любой сигнал со спектром может занимать полосу частот, охватывающую несколько таких поддиапазонов.

Тогда и т.е. сигнал представляет собой сумму некоторого числа элементарных сигналов. В рассматриваемом идеальном случае частотные каналы не перекрываются, поэтому имеет место ортогональность этих элементарных сигналов, т.е.