Курсовая работа: Числа е та пі

1986 рік — 29 360 000 десяткових знаків (Д.Бейли, Cray2),

1987 рік — 134 217 000 десяткових знаків (Я.Канада, NEC SX2),

1989 рік — 1 011 196 691 десяткових знаків (Д.Гудновски й Г.Гудновски, Cray2+IBM3040)"

При обчисленні вірних десяткових знаків числа p користувалися різними способами, деякі, як і Архімед обчислювали периметри вписаних і описаних nбагатогранників, але пізніше стали вдаватися до допомоги рядів. Так Лейбниц обчислював p за допомогою ряду [26]:

Шарп застосував ряд [21]:

Л.Ойлер за допомогою ряду [24]:

Джон Валлис ( 16161703) знайшов нескінченний добуток, за допомогою якого можна обчислити число p (пі), у вигляді [25]:

Число́ пі (позначається ) –математично визначається в Евклідовій геометрії як відношення довжини коладо його діаметру.

Грецька літерапі.

або як площа круга одиничного радіусу.

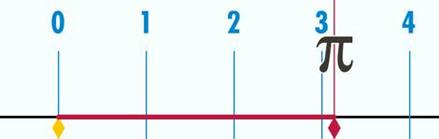
Довжина кола дорівнює p, якщо його діаметр 1

Рис.1.1. Геометричне трактування числа p

Історія числа е (основа експонентної функції).

e — математична константа, основа натурального логарифма, трансцендентне число. Іноді число e називають числом Ойлера або числом Непера [22]. Позначається рядковою латинською буквою «e». Чисельне значення:

e = 2,718 281 828 459 045 235 360 287 471 352 662 497 757

Число e може бути визначено декількома способами [22].

· Через бескінечну межу:

(друга чудова межа).

Як сума ряду:

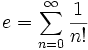або .

Як єдине число a , для якого виконується

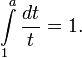
Як єдине позитивне число a , для якого вірно (похідна функції дорівнює самій функції)

Число з'явилося порівняно недавно. Його іноді називають "неперовим числом" на честь винахідника логарифмів шотландського математика Джона Непера ( 15501617) [22], однак це необґрунтовано, тому що немає твердих підстав для твердження, що Непер мав про число е чітке позначення. Уперше математично обгрунтоване позначення числа "е " увів Леонард Ойлер (17071783). Він також обчислив точні 23 десяткові знака цього числа після коми, використавши подання числа е у вигляді нескінченного числового ряду [24]:

,

отримане Данилом Бернулі( 17001782). В 1873 році Ерміт довів трансцендентність числа е . Л.Ойлер одержав чудовий результат, що зв'язує числа е , p :

Йому належить і заслуга визначення функції для комплексних значень z , що поклало початок математичному аналізу в комплексній області теорії функцій комплексного змінного. Ойлером були отримані наступні формули:

Клас логарифмів по основі е , називаються натуральними й позначаються як . Експоненціальна функція з основою е має особливий характер – всі похідні функції дорівнюють самій функції:

1.2 Визначення понять ірраціональності та трансцендентності чисел

Для того щоб довести ірраціональність і транcцендентність чисел і приведемо з початку деякі визначення, теореми й приклади ірраціональних і трансцендентних чисел [9], [11], [20].

Множина дійсних чисел містить у собі підмножину всіх раціональних чисел, тобто чисел, які можна представити у вигляді кінечного дробу, а всі інші дійсні числа називають ірраціональними.

Означення 1.2.1. Дійсне число називається ірраціональним, якщо воно відмінно від всіх раціональних чисел, тобто якщо при всіх цілих і .

Існування ірраціональних чисел було доведено ще грецькими математиками. Ірраціональність числа була відома ще в V столітті до нашої ери математикам пифагорівскої школи, а доказ цього часто приписується Піфагору, хоча точно невідомо, чи було воно побудовано їм самим або кимнебудь із його учнів. Оскільки множину всіх раціональних чисел можна обчислити, основну масу дійсних чисел становлять ірраціональні числа.

Розглянемо найпростіші методи, які дозволяють установлювати ірраціональність деяких класів чисел. На перший погляд здається невиправданим те, що задача доказу ірраціональності якогонебудь дійсного числа а ставиться до теорії чисел, однак включення такої проблематики в теорію чисел стає відразу ясним, якщо поставити це питання в наступній формі: довести, що не існує цілих чисел і , таких, що .

Дамо спочатку одну теорему, що встановлює ірраціональність досить широкого класу дійсних чисел, які зустрічаються особливо часто в шкільних курсах алгебри й геометрії.

Теорема 1.2.1 Нехай багаточлен із цілими коефіцієнтами, дійсне число корінь .Тоді або ціле, або ірраціональне число.