Курсовая работа: Числа е та пі

Теорема 1.4.1.Число ірраціональне.

Доведення. Припустимо, що , де й натуральні числа.Відомо, що

Із треба, що () – було ціле число, тоді цілим буде й число [9]

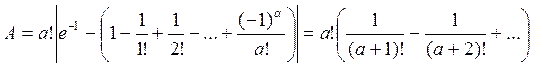
Ми одержуємо звідси ,

Тобто між 0 і 1 лежить ціле число. Припущення, що раціональне, привело нас до протиріччя, значить ірраціональне.

Теорема доведена.

Другий шлях доказу ірраціональності e [23].

Припустимо, що раціонально. Тоді , де — ціле, а — натуральне, звідки

Множачи обидві частини рівняння на , одержуємо

Переносимо в ліву частину:

Всі доданки правої частини цілі, отже:

— ціле

Але з іншої сторони

Знов одержуємо протиріччя.

Трансцендентність була доведена тільки в 1873 році французьким математиком Шарлем Ермітом [22].

Теорема 1.4.2. Число трансцендентно.

Доведення. Припустимо, що корінь багаточлена із цілими коефіцієнтами так що

(1.4.1)

Позначимо через найбільшу з абсолютних величин коефіцієнтів , так що при всіх маємо .

При заданому функція при збільшенні