Курсовая работа: Числа е та пі

з цілими коефіцієнтами. Нехай корінь цього рівняння , одним з них є . Тому що , то

(1.3.11)

Розкривши дужки в лівій частині цієї рівності , одержимо

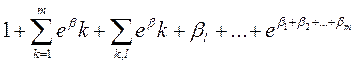(1.3.12)

Позначимо через ті з показників, які відмінні від нуля , а через інші. Приєднавши відповідні доданки в лівій частині (1.3.12) до першого, можемо записати рівність (1.3.12) у вигляді

(1.3.13)

де ціле позитивне число.

Числа суть цілі алгебраїчні числа, тому згідно лемі (1.3.3) цілими алгебраїчними числами є й числа

Дуже важливо помітити , що якщо симетричний багаточлен із цілими коефіцієнтами , те ціле число

Дійсно, якщо

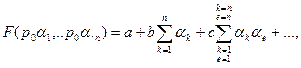
то буде також

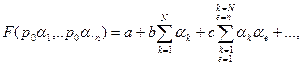
тому що кожна із сум, що коштують у правій частині другої рівності, відрізняється від відповідної суми першої рівності, що складаються або рівними або утримуючого цього числа як множники, а числа дорівнюють нулю.

Вираз в правій частині останньої рівності є симетричним багаточленом відносно й отже , відносно . На підставі теореми [20]: “Якщо симетричний багаточлен із цілими коефіцієнтами й корінь уранения із цілими коефіцієнтами, тjціле число ” , треба, щоб було цілим числом.

Покладемо в рівності (1.3.7) , послідовно , і складемо результати , помноживши попередньо перші з них на .Одержимо на підставі (1.3.13)

(1.3.14)

Якщо ми доведемо, що для деякого багаточлена рівність (1.3.14) неможлива, якщо алгебраїчні числа, то тим самим буде доведена трансцендентність .

Покладемо

(1.3.15)

де просте число, що залишається поки невизначеним. Багаточлен (1.3.15) можна представити у видах

(1.3.16)

Перше з рівностей (1.3.16) безпосередньо отримане з рівності (1.3.15), якщо в правій його частині розкрити дужки. При цьому одержимо

Добуток у правій частині симетричний й тому ціле число. Такі ж, легко зміркувати є й числа .

Друге з рівностей (1.3.16) виходить із рівності (1.3.15) якщо записати його у вигляді

і звільнитися від квадратних дужок. Аналогічно виходить третє з рівностей (1.3.16) і так далі. Важливо помітити, що …є багаточленами із цілими коефіцієнтами відносно

Легко підрахувати, що

(1.3.17)

(1.3.18)

Сума

є симетричним багаточленом із цілими коефіцієнтами й тому є цілим числом. Це число, через (1.3.13) , ділиться на .

Ми будемо вважати більшим кожного із цілих чисел . Тоді

буде цілим числом, яке не ділится на , тому що таким буде перший доданок у правій частині, у той час, як інші доданки будуть цілими числами, що діляться на . Таким чином, сума, що визначена в першій частині рівності (1.3.14), при нашому виборі числа , є цілим числом, що не ділиться на , тобто є відмінним від нуля цілим числом.

Повернемося до розгляду суми

З рівності (1.3.9) , першої рівності (1.3.16) і того , що

легко доглянути, що буде по модулі меншим одиниці, при досить великому .

Таким чином, права частина рівності (1.3.14) є сумою цілого, відмінного від нуля, числа й числа, по модулі меншого одиниці. Така сума не може рівнятися нулю й тому рівності (1.3.14), при нашім виборі й , неможливі. Цим і завершений доказ трансцендентності числа .

Теорема доведена.

1. 4 Доведення ірраціональності та трансцендентності числа „е”