Курсовая работа: Диагностика газовой скважины по результатам гидродинамических исследований при установившейся фильтрации

Степень и характер вскрытия пласта имеют важное значение при разработке месторождений нефти и газа, так как они определяют фильтрационные сопротивления, возникающие в призабойной зоне, и, в конечном итоге, производительность скважин. Выбор степени и характера вскрытия осуществляется в зависимости от физических свойств пластов, их толщины, степени неоднородности, способа разра ботки и т. д. Несовершенство скважин по степени и характеру вскрытия приводит к таким деформациям линий тока, которые приводят к возникновению в призабойной зоне сложных неодномерных течений. В связи с этим рассмотрение особенностей притока к гидродинамически несовершенным скважинам имеет большое практическое значение.

Приток газа к несовершенным скважинам при двучленном законе фильтрации.

Несовершенство газовых скважин при выполнении закона Дарси

(16)

учитывается так же, как несовершенство нефтяных скважин, т. е. радиус скважины в формуле дебита заменяется приведенным радиусом:

(17)

Для расчета дебитов газовых скважин несовершенных по степени и по характеру вскрытия при нарушении закона Дарси может быть предложена следующая схема. Круговой пласт, в центре которого находится скважина, делится на три области (рис. 6).

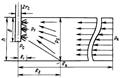
Р ис.6 - Схема притока газа к несовершенной по степени и характеру вскрытия скважине

Первая область имеет радиус R₁ =(2-3)r_с , здесь из-за больших скоростей вблизи перфораци онных отверстий происходит нарушение закона Дарси, т. е. в основном проявляется несовершенство по характеру вскрытия. Линии тока пока заны на рис. 9.

Вторая область представляет собой кольцевое прост ранство R₁ < r< R₂ , R₂ ≈h; здесь линии тока искривляются из-за несовершенства скважины по степени вскрытия, имеет место двучленный закон фильтрации.

В третьей области R₁ < r< R_к , действует закон Дарси, течение можно считать плоскорадиальным. Обозначив давления на границах областей через р₁ и р₂ ,запишем для третьей области в соответствии с формулами нахождения дебита скважины для плоскорадиальной фильтрации:

(18)

Подставив (18) в (19), получим:

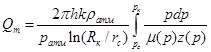(19)

Перейдём к дебиту, приведённому к атмосферному давлению:

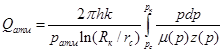(20)

подстам в (20) и получим:

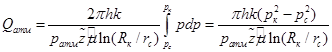(21)

Из уравнения (21) получим течение газа в третьей области

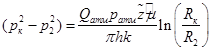(22)

Во второй области примем, что толщина пласта переменна и изменяется по линейному закону от значения bпри r= R₁ до значения hпри r= R₂ , т. е.

z(r) = α+βr(23)

где αиβопределяются из условий z=bпри r=R₁ ,z= hпри r= R₂ .Чтобы получить закон движения в этой области,надо проинтегри ровать уравнение (2), предварительно подставив вместо постоянной толщины hпеременную толщину по формуле (23).

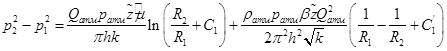(24)

Здесь C₁ и С₁ ^’ - коэффициенты, характеризующие несовершенство скважины по степени вскрытия.

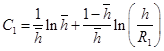(25)

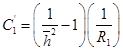, (26)

Обе последние формулы-приближенные, они имеют место при значениях b» R₁ .