Курсовая работа: Диференційні рівняння як основа математичного опису енергетичної системиЕкспертна система контролю

1.2 Математична основа засобу Рунге–Кутта

Засіб Рунге -Кутта можливо получити, якщо разкласти у ряд Тейлора значення у(х)

y(x₀ +h)=y(x₀ )+h(x₀ )h³ +hⁿ yⁿ (x₀ )

x_i =x(0)+Ih

y_i+1 =y_i +∙(K_1i +2K_2i +2K_3i +2K_4i )

K_1i =h∙f(x_i ,y_i )

K_2i =h∙f(x_i +∙y_i +)

K_3i =h∙f(x_i +

K_4i =h∙f(x_i +h∙y_i +K₃ )

Блок - схема головного модуля по Рунге - Кутту:

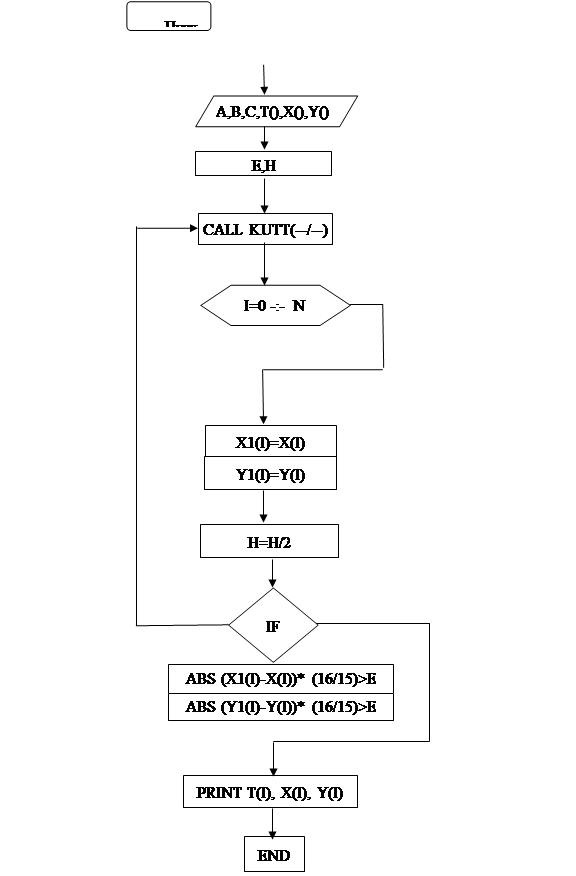
Реалізація програми за засобом Рунге – Кутта. :

DECLARE SUB KUTT (T!, X!, Y!, A%, B%, C%, E!, H!, N%, T(), X(), Y(), K1X!, K1Y!, K2X!, K2Y!, K3X!, K3Y!, K4X!, K4Y!)

DECLARE SUB GRAF (T!, X!, Y!, A%, B%, C%, E!, H!, N%, T(), X(), Y(), K1X!, K1Y!, K2X!, K2Y!, K3X!, K3Y!, K4X!, K4Y!)

INPUT "C"; C%

E! = C% * 10 ^ (-4)

H! = E! ^ (1 / 4)

CONST A% = 0: CONST B% = 1

DIM SHARED T!(2000), X!(2000), Y!(2000), K1X!(2000), K1Y!(2000), K2X!(2000), K2Y!(2000), K3X!(2000), K3Y!(2000), K4X!(2000), K4Y!(2000)

T(0) = 0: X(0) = 0: Y(0) = 0

M1: CALL KUTT(T!, X!, Y!, A%, B%, C%, E!, H!, N%, T(), X(), Y(), K1X!, K1Y!, K2X!, K2Y!, K3X!, K3Y!, K4X!, K4Y!)

FOR I% = 0 TO N%

X1(I%) = X(I%)

Y1(I%) = Y(I%)

NEXT I%

H! = H! / 2

CALL KUTT(T!, X!, Y!, A%, B%, C%, E!, H!, N%, T(), X(), Y(), K1X!, K1Y!, K2X!, K2Y!, K3X!, K3Y!, K4X!, K4Y!)

FOR I% = 0 TO N%

IF ABS(X1(I%) - X(I%)) * (16 / 15) > E! THEN