Курсовая работа: Диференційні рівняння як основа математичного опису енергетичної системиЕкспертна система контролю
T(I%) = T(0) + I% * H!
K1X(I%) = H! * (-2 * X(I%) + 5 * Y(I%))
K1Y(I%) = H! * ((EXP(.5 * Y(I%) + T(I%)) - EXP(-.5 * Y(I%) + T(I%))) / 3 + .5 * Y(I%))
K2X(I%) = H! * (-2 * (X(I%) + K1X(I%) / 2) + 5 * (Y(I%) + K1Y(I%) / 2))
K2Y(I%) = H! * ((EXP(.5 * (Y(I%) + K1Y(I%) / 2) + (T(I%) + H! / 2) - EXP(-.5 * Y(I%) + K1Y(I%) / 2) - (T(I%) + H! / 2))) / 3 + .5 * (Y(I%) + K1Y(I%) / 2))
K3X(I%) = H! * (-2 * (X(I%) + K2X(I%) / 2) + 5 * (Y(I%) + K2Y(I%) / 2))
K3Y(I%) = H! * ((EXP(.5 * (Y(I%) + K2Y(I%) / 2) + (T(I%) + H! / 2) - EXP(-.5 * Y(I%) + K2Y(I%) / 2) - (T(I%) + H! / 2))) / 3 + .5 * (Y(I%) + K2Y(I%) / 2))
K4X(I%) = H! * (-2 * (X(I%) + K3X(I%)) + 5 * (Y(I%) + K3Y(I%)))
K4Y(I%) = H! * ((EXP(.5 * (Y(I%) + K3Y(I%)) + (T(I%) + H!) - EXP(-.5 * Y(I%) + K3Y(I%)) - (T(I%) + H!))) / 3 + .5 * (Y(I%) + K3Y(I%) / 2))
X(I% + 1) = X(I%) + 1 / 6 * (K1X(I%) + 2 * K2X(I%) + 2 * K3X(I%) + K4X(I%))
Y(I% + 1) = Y(I%) + 1 / 6 * (K1Y(I%) + 2 * K2Y(I%) + 2 * K3Y(I%) + K4Y(I%))
NEXT I%
END SUB
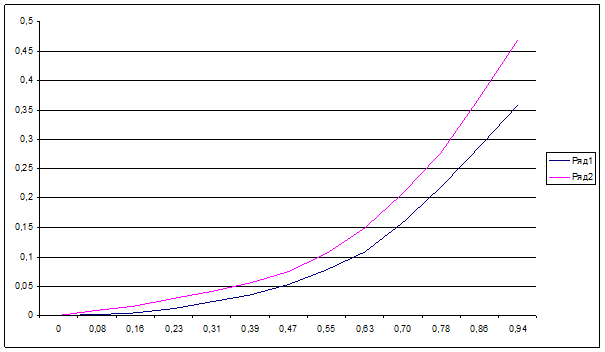
Результати реалізації системи диференційних рівнянь за засобом Рунге – Кутта.
| T | X | Y |
| 0 | 0 | 0 |
| 0,08 | 0,0012 | 0,008075541 |
| 0,16 | 0,00503475 | 0,0157619 |
| 0,23 | 0,0121 | 0,02953131 |
| 0,31 | 0,02278947 | 0,04097326 |
| 0,39 | 0,0349 | 0,05493775 |
| 0,47 | 0,05233831 | 0,07522751 |
| 0,55 | 0,0775 | 0,10523 |
| 0,63 | 0,1089077 | 0,149089 |
| 0,70 | 0,158 | 0,20752 |
| 0,78 | 0,2199285 | 0,2783817 |
| 0,86 | 0,2868 | 0,37033 |
| 0,94 | 0,3583839 | 0,469151 |
Н опт=0,07825423
1.7. Математична основа способу М і лна
Для реалізації засобу Мілна необхідно матиінформацію о попередніх точках. Тому засіб Мілна реалізуєтся післяпідрахунків по засобу Рунге-Кутта з заданной точностью.
Формула прогнозу:
![]()
![]()
![]()
Визначаємо значення проізводної :
Формула коррекції:
Якщо , то
Якщо , то закінчуємо розрахунок і даємо поманду на друк результата .
8.Блок-схема реалізації головного модуля, програми та графічної частини за засобом Мілна
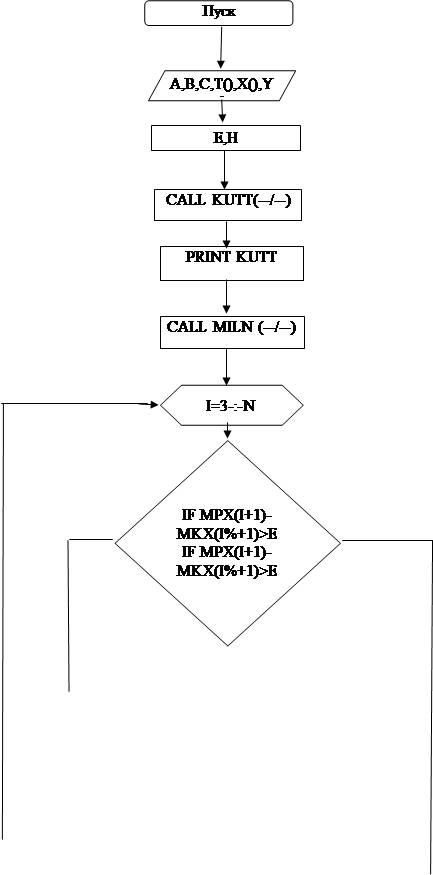 |
нет
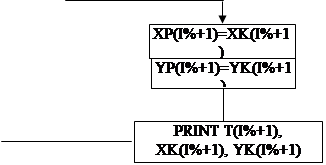 | |
 |
1.9.Реалізація програми за способом Мілна