Курсовая работа: Дисперсионный анализ

С точки зрения техники вычислений для нахождения сумм квадратов Q₁ , Q₂ , Q₃ , Q₄ , Q целесообразнее использовать формулы:

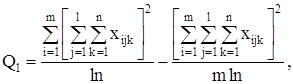
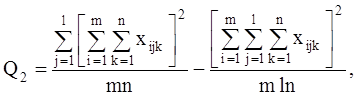
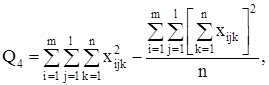
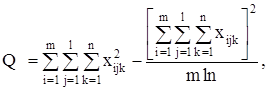
Q₃ = Q – Q₁ – Q₂ – Q₄ .

Отклонение от основных предпосылок дисперсионного анализа — нормальности распределения исследуемой переменной и равенства дисперсий в ячейках (если оно не чрезмерное) — не сказывается существенно на результатах дисперсионного анализа при равном числе наблюдений в ячейках, но может быть очень чувствительно при неравном их числе. Кроме того, при неравном числе наблюдений в ячейках резко возрастает сложность аппарата дисперсионного анализа. Поэтому рекомендуется планировать схему с равным числом наблюдений в ячейках, а если встречаются недостающие данные, то возмещать их средними значениями других наблюдений в ячейках. При этом, однако, искусственно введенные недостающие данные не следует учитывать при подсчете числа степеней свободы /1/.

2 Применение дисперсионного анализа в различных процессах и исследованиях

2.1 Использование дисперсионного анализа при изучении миграционных процессов

Миграция - сложное социальное явление, во многом определяющее экономическую и политическую стороны жизни общества. Исследование миграционных процессов связано с выявлением факторов заинтересованности, удовлетворенности условиями труда, и оценкой влияния полученных факторов на межгрупповое движение населения.

λ_ij =c_i q_ij a_j ,

где λ_ij – интенсивность переходов из исходной группы i (выхода) в новую j (входа);

c_i – возможность и способности покинуть группу i (c_i ≥0);

q_ij – привлекательность новой группы по сравнению с исходной (0≤q_ij ≤1);

a_j – доступность группы j (a_j ≥0).

Если считать численность группы i равной n_i , то оценкой случайной величины ν_ij - числа переходов из i в j – будет n_i c_i q_ij a_j :

ν_ij ≈ n_i λ_ij =n_i c_i q_ij a_j . (16)

На практике для отдельного человека вероятность p перехода в другую группу мала, а численность рассматриваемой группы n велика. В этом случае действует закон редких событий, то есть пределом ν_ij является распределение Пуассона с параметром μ=np:

.

С ростом μ распределение приближается к нормальному. Преобразованную же величину √ν_ij можно считать нормально распределенной.

Если прологарифмировать выражение (16) и сделать необходимые замены переменных, то можно получить модель дисперсионного анализа:

ln√ν_ij =½lnν_ij =½(lnn_i +lnc_i +lnq_ij +lna_j )+ε_ij ,

X_i,j =2ln√ν_ij -lnn_i -lnq_ij ,

C_i =lnc_i ,

A_j =lna_j ,

X_i,j =C_i +A_j +ε.

Значения C_i и A_j позволяют получить модель двухфакторного дисперсионного анализа с одним наблюдением в клетке. Обратным преобразованием из C_i и A_j вычисляются коэффициенты c_i и a_j .

При проведении дисперсионного анализа в качестве значений результативного признака Y следует взять величины:

Y_ij =X_i,j -X,

Х=(Х_1,1 +Х_1,2 +:+Х_mi,mj )/mimj,

где mimj- оценка математического ожидания Х_i,j ;