Содержание

Введение

Глава 1. Теорема о представлении дзета-функции Дедекинда произведением L-рядов Дирихле

Глава 2. Вывод функционального уравнения дзета-функции Дедекинда

Заключение

Список используемой литературы

Введение

В данной работе мы рассмотрим теорему о представлении дзета-функции Дедекинда в виде произведения L-функций и пример приложения этой теоремы к выводу функционального уравнения дзета-функции Дедекинда.

Определим некоторые понятия. Пусть k - конечное расширение поля Q , a - некоторый главный идеал поля k. Рассмотрим его разложение на простые идеалы

где для почти всех p.

Через N (a) обозначим абсолютную норму идеала a, т.е. Определим дзета-функцию Дедекинда :

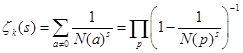
Кроме того каждому характеру сопоставим L-ряд

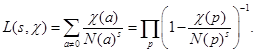
Глава 1. Теорема о представлении дзета-функции Дедекинда произведением L-рядов Дирихле

Докажем следующую теорему

Теорема. Пусть K - конечное абелево расширение поля k; тогда

где произведение справа распространяется на все примитивные характеры, согласованные с характерами группы классов где S - исключительное множество в k, - группа всех идеалов поля k, взаимно простых с S, - подгруппа конечного индекса, образованная теми элементами из , которые содержат нормы относительно k идеалов из K, взаимно простых с S, - подгруппа в подгруппе главных идеалов в , состоящая из таких главных идеалов , для которых и

Доказательство проводится в терминах локальных множителей, причем мы рассмотрим по отдельности неразветвленный и разветвленный случаи.

1. Пусть p - неразветвленный простой идеал из k, т.е.

где - различные простые идеалы в K. Согласно теории полей классов,

где

Поэтому соответствующий локальный множитель слева равен

в то время как соответствующий локальный множитель справа равен

Ввиду того, что f - наименьшее положительное число такое, что для всех, имеет место следующее легко проверяемое тождество

отсюда, если положить, следует нужное равенство.

--> ЧИТАТЬ ПОЛНОСТЬЮ <--