Курсовая работа: Дослідження дзета-функції Римана

, а й . Звідси, підставляючи в подвійну нерівність, маємо

(3). У лівій нерівності покладемо n =0, тоді , тобто . У правом же візьмемо n =1 і одержимо , далі , і, нарешті, . Переходячи в нерівностях до межі при , знаходимо .

Звідси, зокрема, треба, що . Дійсно, покладемо . Тоді , тобто . Тому . З того, що , а , випливає доказуване твердження.

Можна, однак, одержати ще більш точний результат для оцінки поводження дзета-функції в околиці одиниці, чим наведені вище, що належить Дирихле. Будемо відштовхуватися від очевидного при довільному n рівності . Додамо до всіх частин нерівностей (3) суму й віднімемо . Маємо . Нехай тут s прагне до одиниці. За правилом Лопиталя легко обчислити й . Ми поки не знаємо, чи існує межа вираження при , тому, скориставшись найбільшою й найменшою межами, напишемо нерівності так:

. Через довільність n візьмемо . Перше й останнє вираження прагнуть до Ейлерової постійного C (C 0,577). Виходить, а, отже, існує й звичайна межа й .

Знайдені вище межі дозволяють одержати лише приблизне подання про вид графіка дзета-функції. Зараз ми виведемо формулу, що дасть можливість нанести на координатну площину конкретні крапки, а саме, визначимо значення , де k – натуральне число.

Візьмемо відоме розкладання , де - знамениті числа Бернуллі (по суті, через нього ці числа й визначаються). Перенесемо доданок у ліву частину рівності. Ліворуч одержуємо cth , а в правій частині - , тобто cth . Заміняємо на , одержуємо cth .

З іншого боку, існує рівність cth , з якого cth . Підстановкою замість знаходимо cth. Якщо , то для будь-якого N і по теоремі про додавання нескінченної множини статечних рядів cth.

Дорівняємо отримані розкладання:

, отже . Звідси негайно треба формула

(4), де - k-е число Бернуллі. Вона зручна тим, що ці числа добре вивчені й для них складені великі таблиці.

Тепер, виходячи з отриманих результатів, можна побудувати ескіз графіка дзета-функції Римана, що досить добре відбиває її поводження на всій області визначення.

Леонард Ейлер, що вперше розглянув дзета-функцію, одержав чудове розкладання її в нескінченний добуток, що іноді теж приймають за визначення:

, де p_i – i-е простої число (4).

Доведемо тотожність ряду (1) і добутку (4). Згадавши формулу суми геометричної прогресії, одержуємо рівність

Якщо перемножити кінцеве число таких рядів, що відповідають всім простим числам, що не перевершують заданого натурального числа N , то частковий добуток, що вийшов, виявиться 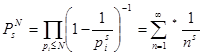рівним , де символ * означає, що підсумовування поширюється не на всі натуральні числа, а лише на ті з них (не вважаючи одиниці), які у своєму розкладанні містять тільки прості числа менші N. Тому що перші N натуральних чисел цією властивістю володіють, то

(5).

Сума містить не всі числа, більші N +1, тому, мабуть, . З (5) одержуємо

(6).

Через збіжність ряду (1), вираження праворуч, що представляє його остача після N-Го члена, прагне до нуля при N прагнучої до нескінченності, а є добуток (4). Значить із нерівності при 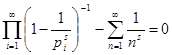, що й було потрібно довести.

Формула (4) важлива тому, що вона зв'язує натуральний ряд, представлений множиною значень аргументу дзета-функції, із множиною простих чисел. Ще один крок у цьому напрямку ми зробимо, оцінивши , а саме показавши, що , де залишається обмеженим при .

З (4) треба, що 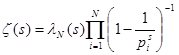, де N, а при . Візьмемо логарифм від обох частин рівності, тоді . Натуральні логарифми під знаком суми розкладаються в ряд: 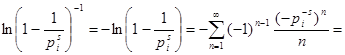. Підставивши отримані розкладання в рівність і спрямувавши N до нескінченності, маємо 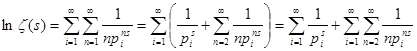. Залишається довести обмеженість останнього доданка. Ясно, що . Остання рівність справедливо, тому що . Далі, мабуть, , що й завершує доказ.

На цьому закінчимо виклад властивостей дзета-функції Римана для дійсного аргументу, тому що найбільший теоретичний і прикладний інтерес представляє випадок викладений у другому розділі.

Розділ 2

Всі результати першого розділу, що стосуються дзета-функції Римана, були отримані в припущенні, що її аргумент s – дійсне число. Однак, найвидатніші дослідження й численні важливі додатки стали можливі лише після включення в область визначення функції комплексних чисел. Уперше розглянув дзета-функцію як функцію мнимого аргументу німецький математик Бернгард Риман, що глибоко вивчив її властивості й широко застосовував її в теорії чисел. На честь його функція одержала свою назву.

Для комплексної дзета-функції залишається в силі визначення, дане в главі 1, з тією лише зміною, що тепер там буде C. Виникає необхідність знайти нову область визначення. Із цією метою доведемо наступне твердження: у напівплощині ( дійсна частина числа x ) ряд

(1) сходиться абсолютно.

Нехай . Підрахуємо абсолютні величини членів ряду (1), . Перший множник містить тільки речовинні числа й , тому що . До другого ж множника застосуємо знамениту формулу Ейлера, одержимо . Виходить, . Через збіжність ряду при α>1, маємо абсолютну збіжність ряду (1).