Курсовая работа: Дослідження дзета-функції Римана

Неважко показати, що всі отримані для дзета-функції формули без змін переносяться на випадок комплексного аргументу. Доказу перетерплюють незначні перетворення, пов'язані з переходом до абсолютних величин.

У зв'язку із цим зауваженням стає можливим використовувати розкладання дзета-функції в добуток 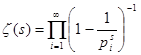, де s тепер будь-яке комплексне число, таке, що . Застосуємо його до доказу відсутності у функції корінь.

Оцінимо величину , використовуючи властивість модуля : 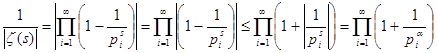, де як звичайно . Тому що 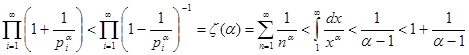, те, а , отже, дзета-функція в нуль не звертається.

Питання про нулі дзета-функції, а також інші прикладні питання одержують нові широкі можливості для дослідження, якщо поширити її на всю комплексну площину. Тому, зараз ми одним з багатьох можливих способів знайдемо аналітичне продовження дзета-функції й виведемо її функціональне рівняння, що характеризує й однозначно визначальне .

Для цього нам знадобиться формула

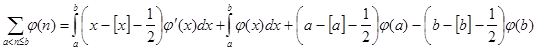(2), що виводиться в такий спосіб. Використовуючи властивості інтегралів можна записати 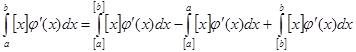. Для будь-якого d при , значить 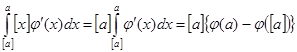і , а . . Отже, . Інтеграл можна знайти інтегруванням вроздріб, приймаючи , ; тоді , а . У результаті . Віднімемо із цього інтеграла попередній і одержимо , звідси легко треба рівність (2).

Тепер покладемо в (2) , , a і b – цілі позитивні числа. Тоді . Нехай спочатку , приймемо a =1, а b спрямуємо до нескінченності. Одержимо . Додамо по одиниці в обидві частини рівностей:

(3).

Вираження є обмеженим, тому що , а функція абсолютно інтегрувальна на проміжку при , тобто при , . Виходить, інтеграл абсолютно сходиться при , причому рівномірно в будь-якій кінцевій області, що лежить у комплексній площині праворуч від прямої . Тим самим він визначає аналітичну функцію змінної s , регулярну при . Тому права частина рівності (3) являє собою аналітичне продовження дзета-функції на напівплощину й має там лише один простий полюс у крапці з відрахуванням, рівним одиниці.

Для можна перетворити вираження (3) дзета-функції. При маємо , виходить, і . Тепер при (3) може бути записане у вигляді .

Небагато більше складними міркуваннями можна встановити, що в дійсності (3) дає аналітичне продовження дзета-функції на напівплощину . Покладемо , а , тобто первісна для . обмежено, тому що , а інтеграл і обмежений через те, що . Розглянемо інтеграл при x₁ >x₂ і . Інтегруємо його вроздріб, прийнявши , , тоді , а по зазначеному вище твердженню . Одержуємо 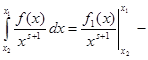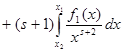. Візьмемо , а . Маємо , , тому що є обмеженою функцією. Виходить,

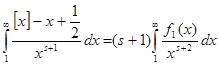(4).

Користуючись абсолютною збіжністю інтеграла , якщо , і обмеженістю функції , робимо висновок, що в лівій частині рівності (4) інтеграл теж сходиться при . Значить формулою (3) можна продовжити дзета-функцію й на напівплощину правіше прямій .

Неважко встановити, що для негативних 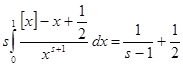, тому з (3) маємо

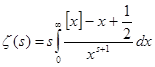(5) при .

З теорії рядів Фур'є відомо, що для нецілих значень x справедливе розкладання в ряд

(6).

Підставимо його в рівність (5) і інтегруємо ряд:

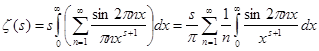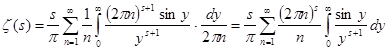. Зробимо в отриманому інтегралі підстановку , звідси треба , а , і одержимо далі . Відомо, що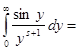 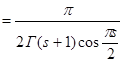, значить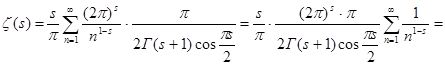 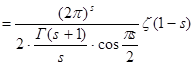. З відомого співвідношення для гамма-функції , по формулі доповнення , отже

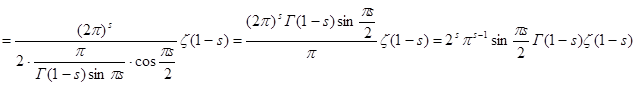
Отже, ми одержали функціональне рівняння дзета-функції Римана

(7),

яке саме по собі може служити засобом вивчення цієї функції, тому що цілком характеризує її, у тому розумінні, що будь-яка інша функція , що задовольняє рівності (7), а також ще деяким природним умовам, тотожна с.

Поки, щоправда, як треба з міркувань, ми довели формулу (7) для . Однак права частина цієї рівності є аналітичною функцією s і при . Це показує, що дзета-функція може бути аналітично продовжена на всю комплексну площину, причому не має на ній ніяких особливостей, крім згадуваного полюса при .

Щоб доказ був строгим, ми повинні ще обґрунтувати по членне інтегрування. Оскільки ряд (6) сходяться майже всюди і його часткові суми залишаються обмеженими, по членне інтегрування на будь-якому кінцевому відрізку припустимо. Через 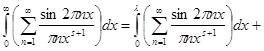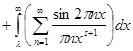для кожного , залишається довести, що 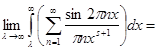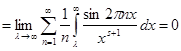при . Але інтегруючи внутрішній інтеграл вроздріб маємо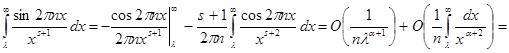

. Звідси без праці виходить наше твердження.

Функціональне рівняння дзета-функції (7) може бути записано багатьма способами. Наприклад, замінимо s на 1-s , одержуємо рівносильну рівність

(8). З нього можна одержати два невеликих наслідки.

Підставимо в (8) замість s число 2m , де m – натуральне число. Маємо . По формулі (4) першого розділу , а , тому й зробивши в правій частині всі скорочення, з огляду на, що , одержимо .

Покажемо ще, що . Для цього логарифмуємо рівність (8): і результат диференціюємо . В околиці крапки s =1 , , , де З – постійна Ейлера, а k – довільна постійна. Отже, спрямовуючи s до одиниці, одержимо, тобто . Знову з формули (4) глави 1 при k =0 , виходить, дійсно, .