Курсовая работа: Дослідження дзета-функції Римана
Як уже було сказано, дзета-функція Римана широко застосовується в математичному аналізі. Однак найбільше повно важливість її виявляється в теорії чисел, де вона надає неоціненну допомогу у вивченні розподілу простих чисел у натуральному ряді. На жаль, розповідь про серйозні й нетривіальні застосування дзета-функції Римана виходить за рамки цієї роботи. Але щоб хоча б небагато представити міць цієї функції, доведемо з її допомогою кілька цікавих тверджень.
Наприклад, відомо, що простих чисел нескінченно багато. Самий знаменитий елементарний доказ належить Евклиду. Воно полягає в наступному. Припустимо, що існує кінцеве число простих чисел, позначимо їх p1 , p2 , … , pn ... Розглянемо число p1 p2 …pn +1,воно не ділиться на жодне із простих і не збігається з жодним з них, тобто є простим числом, відмінним від вищевказаних, що суперечить припущенню. Виходить, кількість простих чисел не може бути кінцевим.
Інший доказ цього факту, що використовує дзета-функцію, було дано Ейлером. Розглянемо дане в першому розділі рівність (5) при s =1, одержимо  , звідси
, звідси  й через гармонійний ряд, маємо при
й через гармонійний ряд, маємо при ![]()
 (1). Якби кількість простих чисел бути кінцевим, то й цьому добутку мало кінцеве значення. Однак, отриманий результат свідчить про зворотний. Доказ завершений.
(1). Якби кількість простих чисел бути кінцевим, то й цьому добутку мало кінцеве значення. Однак, отриманий результат свідчить про зворотний. Доказ завершений.
Тепер перепишемо (1) у вигляді  . Опираючись на теорему про збіжність нескінченного добутку, з попереднього робимо висновок, що ряд
. Опираючись на теорему про збіжність нескінченного добутку, з попереднього робимо висновок, що ряд ![]() розходиться. Ця пропозиція дає деяку характеристику росту простих чисел. Підкреслимо, що воно набагато сильніше твердження про гармонійний ряд, тому що тут мова йде лише про частину його членів, тим більше що в натуральному ряді є як завгодно довгі проміжки без простих чисел, наприклад:
розходиться. Ця пропозиція дає деяку характеристику росту простих чисел. Підкреслимо, що воно набагато сильніше твердження про гармонійний ряд, тому що тут мова йде лише про частину його членів, тим більше що в натуральному ряді є як завгодно довгі проміжки без простих чисел, наприклад: ![]() ,
, ![]() , … ,
, … , ![]() ...
...
Незважаючи на свою простоту наведені вище пропозиції важливі в концептуальному плані, тому що вони починають низку досліджень усе більше й більше глибоких властивостей ряду простих чисел, що триває донині. Спочатку, основною метою вивчення дзета-функції саме й було дослідження функції ![]() , тобто кількості простих чисел не переважаючих x . Як приклад формули, що зв'язує
, тобто кількості простих чисел не переважаючих x . Як приклад формули, що зв'язує ![]() й
й ![]() , ми зараз одержимо рівність
, ми зараз одержимо рівність
![]() (2).
(2).
Спочатку скористаємося розкладанням дзета-функції в добуток:  . З логарифмічного ряду
. З логарифмічного ряду ![]() , з огляду на, що
, з огляду на, що  , приходимо до ряду
, приходимо до ряду 
 . Виходить,
. Виходить, ![]() .
.
Тепер обчислимо інтеграл у правій частині (2). Тому що при ![]()
![]() , те
, те  . У внутрішньому інтегралі покладемо
. У внутрішньому інтегралі покладемо ![]() , тоді
, тоді ![]() й
й  , звідси
, звідси  .У проміжку інтегрування
.У проміжку інтегрування ![]() , тому вірно розкладання
, тому вірно розкладання ![]() й
й ![]()
![]() . Одержуємо
. Одержуємо 
 . Тепер
. Тепер 
![]()
![]() . Якщо зрівняти отримане значення інтеграла з поруч для
. Якщо зрівняти отримане значення інтеграла з поруч для ![]() , то побачимо, що вони тотожні й рівність (2) доведено.
, то побачимо, що вони тотожні й рівність (2) доведено.
Використовуємо формулу (2) для доказу однієї дуже серйозної й важливої теореми, а саме одержимо закон розподілу простих чисел, тобто покажемо, що ![]() .
.
Як історична довідка відзначу, що великий німецький математик Карл Фрідріх Гаус емпірично встановив цю закономірність ще в п'ятнадцятирічному віці, коли йому подарували збірник математичних таблиць, що містить таблицю простих чисел і таблицю натуральних логарифмів.
Для доказу візьмемо формулу (2) і спробуємо дозволити це рівняння відносно ![]() , тобто звернути інтеграл. Зробимо це за допомогою формули обігу Мелина в такий спосіб. Нехай
, тобто звернути інтеграл. Зробимо це за допомогою формули обігу Мелина в такий спосіб. Нехай ![]()
![]() . Тоді
. Тоді
![]() (3). Цей інтеграл має потрібну форму, а
(3). Цей інтеграл має потрібну форму, а ![]() не вплине на асимптотику
не вплине на асимптотику ![]() . Дійсно, тому що
. Дійсно, тому що ![]() , інтеграл для
, інтеграл для ![]() сходиться рівномірно в напівплощині
сходиться рівномірно в напівплощині ![]() , що легко виявляється порівнянням з інтегралом
, що легко виявляється порівнянням з інтегралом 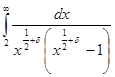 . Отже,
. Отже, ![]() регулярна й обмежена в напівплощині
регулярна й обмежена в напівплощині ![]() . Те ж саме справедливо й відносно
. Те ж саме справедливо й відносно ![]() , тому що
, тому що ![]()
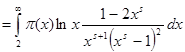 .
.
Ми могли б уже застосувати формулу Меллина, але тоді було б досить важко виконати інтегрування. Тому колись перетворимо рівність (3) у такий спосіб. Диференціюючи по s , одержуємо ![]() . Позначимо ліву частину через
. Позначимо ліву частину через ![]() і покладемо
і покладемо 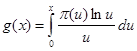 ,
, 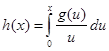 , (
, (![]() ,
, ![]() і
і ![]() думаємо рівними нулю при
думаємо рівними нулю при ![]() ). Тоді, інтегруючи вроздріб, знаходимо
). Тоді, інтегруючи вроздріб, знаходимо  при
при ![]() , або
, або 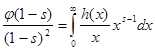 .
.
Але ![]() безперервна й має обмежену варіацію на будь-якому кінцевому інтервалі, а тому що
безперервна й має обмежену варіацію на будь-якому кінцевому інтервалі, а тому що ![]() , те
, те ![]() (
(![]() ) і
) і ![]() (
(![]() ). Отже,
). Отже, ![]() абсолютно інтегрувальна на
абсолютно інтегрувальна на ![]() при
при ![]() . Тому
. Тому 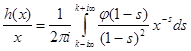 при
при ![]() , або
, або 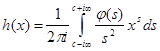 при
при ![]() . Інтеграл у правій частині абсолютно сходиться, тому що
. Інтеграл у правій частині абсолютно сходиться, тому що ![]() обмежено при
обмежено при ![]() , поза деякою околицею крапки
, поза деякою околицею крапки ![]() . В околиці
. В околиці ![]()
![]()