Курсовая работа: Дослідження методів чисельного інтегрування
Площа кожної такої трапеції визначається за формулою Сімпсона:
Si= ![]() [f(xi)+4f(
[f(xi)+4f(![]() xi+1)+f(xi+2)], (1.6), тобто
xi+1)+f(xi+2)], (1.6), тобто
 (y0 +4y1 +y2 ),
(y0 +4y1 +y2 ),
 (y2 +4y3 +y4 ),
(y2 +4y3 +y4 ),
 (y4 +4y5 +y6 ), (1.7)
(y4 +4y5 +y6 ), (1.7)
. . . . . . . . . . . . . . . . . . . . . . .
 (y2n-2 +4y2n-1 +y2n ),
(y2n-2 +4y2n-1 +y2n ),
Тоді чисельне значення визначеного інтеграла на відрізку [a,b] дорівнюватиме сумі інтегралів, тобто
 [y0 +y2n +4(y1 +...+y2n-1 )+2(y2 +...+y2n-2 )],
[y0 +y2n +4(y1 +...+y2n-1 )+2(y2 +...+y2n-2 )],
або
 [y0 +y2n +4
[y0 +y2n +4![]() y2i-1 +2
y2i-1 +2![]() y2i ],(1.8)
y2i ],(1.8)
де h =(b-a)/2N.
Похибка обчислення інтеграла за формулою Сімпсона оцінюється як
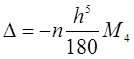
де М4 –максимальне значення четвертої похідної. f(x) при ![]() , h- крок обчислень.
, h- крок обчислень.
1.4 Метод Ньютона-Котеса
Цей метод засновано на апроксимації однієї із сторін криволінійної трапеції, яка отримується поділом відрізка [a,b] на N рівних частин, многочленами вищих порядків, також як у методі трапецій використовується лінійна апроксимація (заміна однієї із сторін трапеції прямою лінією), а в методі Сімпсона - апроксимація параболою.
Основна формула методу:
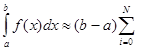 yi Hi, (1.9)
yi Hi, (1.9)
де Hi - коефіцієнти Ньютона - Котеса. Ці коефіцієнти не залежать від вигляду f(x), а є функцією тільки N (кількість вузлів інтерполяцїї). Таким чином, коефіцієнти Ньютона - Котеса можна обчислити раніше для різного числа вузлів інтерполяції .
Легко можна показати, що методи трапецій та Сімпсона є частинними випадками методу Ньютона - Котеса.
1.5 Метод Чебишева
Метод Чебишева використано в курсовій грунтується на обчисленні інтеграла за значеннями функції yi =f(xi),(i=1,2,...,N) у зафіксованих вузлах інтерполяції x1,x2,...,xN (де h=const). Коефіцієнти Ньютона -Котеса Нi (i=1,N) не залежать від значень функції у вузлах інтерполяції. П.Л.Чебишев запропонував для обчислення визначених інтегралів використати формулу:
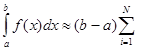 ci f(xi ), (1.10)
ci f(xi ), (1.10)
в якій квадратурні коефіцієнти сi (i = 1,2, ...,N) зафіксовані, а абсциси xi (i=1,2,...,N)підлягаютьвизначенню.
Таблиця 1.1.
Коефіцієнти Ньютона - Котеса
| n = 1 | Но = H1 = ½ | |
| n = 2 | Но = Н2 = 1/6, Н1 = 2/3 | |
| n = 3 | Н0 = Н3 = 1/8, Н1 = H2 = 3/8 | |
| n = 4 | Но = Н4 = 7/90, Н1 = Нз = 16/45, Н2 = 2/15 | |
| n = 5 |
Н0 = Н5 =19/288, Н1 = Н4 = 25/96, Н2 = Нз = = 25/144 | |
| n = 6 | Но = Н6 = 41/840, Н1 = Н5 = 9/35, Н2 = Н4 = =9/280, Нз = 34/105 | |
| n = 7 | Но = Н7 = 75І/17280, Н1 = Н6 = 3577/1728О, Н2 = Н5 =1323/1728О, Нз = Н4 = 2989/17280 | |