Курсовая работа: Дослідження методів чисельного інтегрування
2Cn[f(x1 )+f(x2 )+...+f(xn )],(1.11)
де квадратурні коефіцієнти Сn та абсциси xi підлягають визначенню.
Коефіцієнти та вузли інтерполяції xi визначимо із умови, що ця рівність є точною для випадку, коли f(х) многочлен вигляду:
f(x)=a0 +a1 x+a2 x2 +...+an xn .(1.12)
Підставимо многочлен у ліву частину попередньої формули та про- інтегруємо:
(a0 +a1 x+a2 x2 +...+an xn )=2(a0 +
a2 +
a3 +...).(1.13)
У праву частину рівності (1. 11) підставимо значення многочлена (1.І2) у вузлах x1,x2,...,xn:
f(x1 )=a0 +a1 x1 +a2 x1 2 +a3 x1 3 +...+an x1 n ,
f(x2 )=a0 +a1 x2 +a2 x2 2 +a3 x2 3 +...+an x2 n ,
f(x3 )=a0 +a1 x3 +a2 x3 2 +a3 x3 3 +...+an x3 n ,(1.14)
. . . . . . . . . . . . . . . . . . . . . . . . . . . . .
f(xn )=a0 +a1 xn +a2 xn 2 +a3 xn 3 +...+an xn n ,
Тоді рівність (1.ІЗ) набере вигляду:
2(a0 +a2 +a4 +...)=2cn [na0 +a1 (x1 +x2 +...+xn )+a2 (x1 2 +x2 2 +...+xn 2 )+
+a3 (x1 3 +x2 3 +...+xn 3 )+...+an (x1 n +x2 n +...+xn n )].(1.15)
Отримана рівність повинна виконуватися за будь-яких значень a0 ,a1 ,...,an ; таким чином, порівнюючи коефіцієнти аi в правій та лівій частинах (1.І5) знаходимо, що nсn = 1, звідки
Cn =
.(1.16)
і, крім цього,
x1 +x2 +x3 +...+xn =0,
x1 2 +x2 2 +x3 2 +...+xn 2 =
,
x1 3 +x2 3 +x3 3 +...+xn 3 =0,(1.17)
x1 4 +x2 4 +x3 4 +...+xn 4 =
,
. . . . . . . . . . . . . . . . . . .
x1 n +x2 n +x3 n +...+xn n =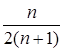
[1-(-1)n+1 ],
Підставляючи знайдене для Сn виразу в співвідношені 1.13 отримаємо формулу Чебишева:
[f(x1 )+f(x2 )+...+f(xn )],(1.18)
де точки x1,...,хn визначаються із системи рівнянь (1.17).
Значення x1,...,хn для різних n обчислюються раніше та зводять в табл. 1.2.
Коли межі даного інтеграла відрізняються від -1 та 1, формула Чебишева матиме вигляд: