Курсовая работа: Дослідження властивостей лiнiйних динамічних кіл
Оскільки ![]() , тому перехідний процес, а отже і перехідна характеристика, повинні мати аперіодичний характер.
, тому перехідний процес, а отже і перехідна характеристика, повинні мати аперіодичний характер.
Переходячи від зображення (1.5) до оригіналу перехідної характеристики маємо:
![]() (1.6)
(1.6)
де ![]() ,
, ![]() ,
,
![]() ,
, ![]() .
.
Імпульсна характеристика як похідна по часу від перехідної:
![]() (1.7)
(1.7)
Графік перехідної характеристики показано на рис 1.2,а; імпульсної – на рис 1.2,б. Результати розрахунків ![]() і
і ![]() вказані в таблиці 1.1.
вказані в таблиці 1.1.
Таблиця 1.1 Значення перехідної та імпульсної характеристик
| 0 | 10 | -9.965 |
| 3,00000 | 4.216 | -3.03 |
| 6,00000 | 2.37 | -1.059 |
| 9,00000 | 1.658 | -0.475 |
| 12,0000 | 1.295 | -0.283 |
| 15,0000 | 1.056 | -0.205 |
| 18,0000 | 0.874 | -0.162 |
| 21,0000 | 0.728 | -0.133 |
| 24,0000 | 0.607 | -0.11 |
| 27,0000 | 0.506 | -0.092 |
| 30,0000 | 0.422 | -0.076 |
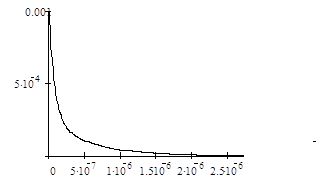
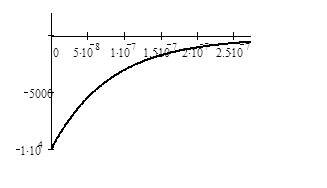
Рисунок 1.2 – Перехідна (а) та імпульсна (б) характеристики
Тепер знайдемо реакцію на сигнал довільної форми (рис. А.2).
Ураховуючи те, що діючий сигнал має різні функціональні залежності від часу на різних часових відрізках, визначимо реакцію на цей сигнал методом припасовування.
Розглянемо проміжок часу ![]() , де
, де ![]() .
.
На цьому проміжку вхідний сигнал: 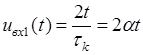 .
.
Згідно з методом перехідних характеристик реакція має вигляд:
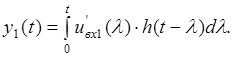
Далі розглянемо проміжок часу ![]() , де
, де ![]() .
.
На цьому проміжку математична модель вхідного сигналу має вигляд:
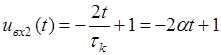 .
.
Тоді реакція, знайдена за інтегралом Дюамеля, має вигляд:
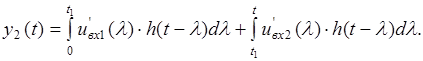
На проміжку часу ![]() вхідний сигнал:
вхідний сигнал: ![]() .
.
Тоді реакція, знайдена за інтегралом Дюамеля, має вигляд:
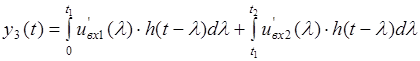
Повна реакція кола на діючий сигнал:
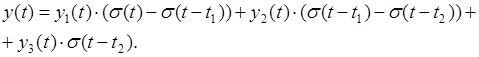 (1.8)
(1.8)
Графік реакції на рис. 1.3, а числові дані в таблиці 1.2.