Курсовая работа: Дослідження властивостей лiнiйних динамічних кіл

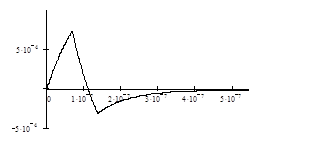
Рисунок 1.3 – Значення реакції кола на трикутний імпульс

Перевіримо отриманий результат графічною інтерпретацією процедури розрахунків методом інтеграла Дюамеля. Використаємо для цього формулу інтеграла Дюамеля через імпульсну характеристику (1.1). Відповідно до формули (1.1) миттєвим значенням реакції для моментів часу відповідає площа, яка є алгебраїчною сумою двох площ: перша – це площа фігури, яка обмежується віссю абсцис і графіком функції, отриманої в результаті добутку зсунутого в точку на осі абсцис дзеркального відображення відносно осі координат неперервної складової (без стрибка) імпульсної характеристики та діючого сигналу; друга – пропорційна добутку початкового значення перехідної характеристики на миттєве значення .

Розглянемо момент часу . Графіки вхідного сигналу та відповідно копії імпульсної характеристики на рис.1.4,а.

Очевидно, що добуток цих функцій дорівнює дорівнює нулю, а отже дорівнює дорівнює нулю і перша площа . Таким чином, початкове значення реакції також дорівнює нулю .

Розглянемо момент часу . Графіки вхідного сигналу та відповідно копії імпульсної характеристики на рис.1.4,б. Реакція в цей момент часу зростає. Площа дорівнює .

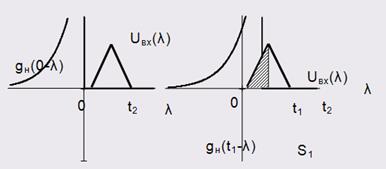
Рисунок 1.4

Розглянемо момент часу . Графіки вхідного сигналу та відповідної копії імпульсної характеристики (рис.1.5,а). Для даного моменту часу , а отже площа від’ємна [4].

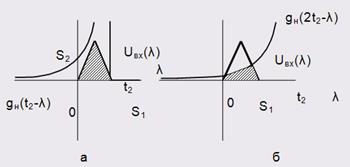
Рисунок 1.5

Розглянемо момент часу . Графіки вхідного сигналу та відповідної копії імпульсної характеристики (рис.1.5,б). Для даного часу друга площа є від’ємною, але значно меншою ніж у попередніх випадках. Очевидно, що при подальшому зсуві копії імпульсної характеристики, виходячи з її виду, площа буде зменшуватися, все більше наближаючись до нуля. А отже, знайдена нами реакція обчислена вірно.

2. Визначення частотних характеристик заданого кола

Вимоги на частотні властивості системи та її складові визначаються через відповідні параметри так званих частотних характеристик.

Частотні характеристики отримують на основі комплексної частотної функції (КЧФ) кола:

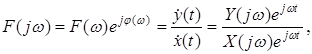(2.1)

де - амплітуда діючого комплексного експоненціального сигналу , - амплітуда реакції такого ж виду, як і дія є у загальному випадку величинами комплексними та функціями дійсної частоти чи .

Ці амплітуди можуть бути виражені через параметри гармонічної реакції та дії: - комплексна амплітуда дії, - комплексна амплітуда реакції.

Залежність виду називають амплітудно-частотною характеристикою (АЧХ) лінійного кола, а - його фазо-частотною характеристикою (ФЧХ). Ця пара характеристик лінійного динамічного кола визначає його властивості в області дійсної частоти чи в усталеному гармонічному режимі.

Отже, знаходження частотних характеристик кола зводиться до визначення комплексної частотної функції кола.

Реакція лінійного електричного кола на гармонічний сигнал (дію) в моменти часу, коли всі процеси визначаються тільки діючим сигналом, теж є гармонічною, причому амплітуда реакції .

Графічне зображення комплексної частотної функції , яка зветься амплітудно-фазовою характеристикою або частотним годографом - це геометричне місце точок на комплексній площині кінця радіус-вектора довжиною, що дорівнює модулю КЧФ , та кутом нахилу до дійсної осі, що дорівнює значенню її аргументу, для відповідних значень частоти при її зміні від нуля до нескінченості.

Амплітудно-частотна характеристика - це модуль

КЧФ для різних значень частоти .

Фазо-частотна характеристика - аргумент КЧФ.

Характеристика затримки чи групового часу запізнення характеризує швидкість зміни ФЧХ:

Дійсна частина КЧФ — дійсна АЧХ, а її уявна частина - уявна АЧХ.