Курсовая работа: Дрейфовые транзисторы их параметры, преимущества и недостатки

Зависимость коэффициента передачи тока от тока коллектора.

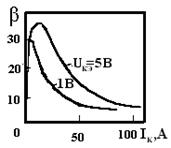
Рис. 2.2.2

Спад β в области малых токов обусловлен рекомбинацией носителей заряда в ОПЗ эмиттера от тока коллектора(третий член), а спад β в области больших токов—уменьшением коэффициента инжекции (второй член). Кроме явной зависимости β(I_nx ) необходимо иметь в виду, что постоянная накопления τ_F резко возрастает в области больших токов из-за влияния эффекта Кирка и квазинасыщения. Возрастание τ_F и уменьшение i_k.f == Q_B0 / τ_F в области больших токов усиливают спад β.

Зависимость коэффициента передачи тока β от напряжения коллектор—эмиттер U_кэ обусловлена рядом эффектов, связанных с изменением границы ОПЗ коллекторного перехода x_1к при изменении U_кэ . При малых плотностях тока основную роль играет расширение ОПЗ коллектора в область базы, за счет чего изменяется толщина квазиэлектронейтральной базы (эффект Эрли). В области повышенных плотностей тока и небольших напряжений Uкэ начинает сказываться эффект Кирка и эффект квазинасыщения. При больших обратных напряжениях U_КЭ дополнительное возрастание β связано с явлением лавинного размножения носителей заряда в ОПЗ коллектора.

3. Влияние неравномерного распределения примесей в базе на параметры дрейфового транзистора

Увеличение скорости движения носителей через базу в первую очередь уменьшает пролетное время. Влияние дрейфового поля проявляется и в выравнивании скоростей носителей. Разброс в скоростях и этом случае оказывается не так высок, как в случае чисто диффузионного движения, где все определяется только тепловыми скоростями. В результате падение коэффициента переноса β до уровня 0,707 должно произойти на частоте, существенно превышающей частоту юр бездрейфового транзистора с той же толщиной базы.

Увеличение предельной частоты приводит к изменению основных фазовых соотношений. Фазовый сдвиг на частоте юр оказывается несколько больше, чем для бездрейфового транзистора. Формула для частотной зависимости коэффициента переноса примет вид

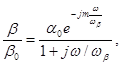(3.1)

где т =0,5— 0,8, β-коэффициент переноса.

Расчетным путем получено и подтверждено экспериментально, что для большинства дрейфовых транзисторов, германиевых и кремниевых, т =0,6. Фазовый угол φ_β может быть рассчитан из соотношения

(3.2)

где К=0,5·ln(N_Э /N_К )-показатель перепада концентрации.

Зависимость предельной частоты ƒ_β от перепада концентрации может быть аппроксимирована одним из следующих выражений[5]:

(3.3)

или

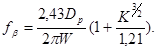(3.4)

Так как множитель перед скобками представляет собой предельную частоту коэффициента-переноса бездрейфового транзистора ƒ_β0 , то (3.3) и (3.4) можно переписать в следующем виде:

(3.5)

Или

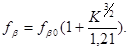(3.6)

Первое выражение проще, но хорошо отражает зависимость ƒ_β от перепада концентрации только при N_Э /N_К > 100. Второе выражение дает лучшую аппроксимацию в более широком диапазоне изменения перепада концентраций.

Полагая N_Э = 10¹⁷ см^-3 и N_К = 10¹⁴ см^-3 (N_Э /N_К = 1000), получаем, что предельная частота коэффициента переноса дрейфового транзистора будет в этом случае более чем в 6 раз превышать предельную частоту коэффициента переноса бездрейфового транзистора.

Поскольку дрейфовые транзисторы могут иметь очень высокие значения предельной частоты ƒ_β , то расчеты показывают, что в этом случае уже нельзя полагать эффективность эмиттера частотно-независимой и считать, что ƒ_β ≈ f_a . Так как эмиттерный переход шунтирован зарядной емкостью, то на достаточно высоких частотах токи смещения через переход могут оказаться соизмеримыми с токами инжекции.

Для того чтобы оценить роль эффективности эмиттера, рассмотрим конкретный пример транзистора типа р-п-р с концентрацией у эмиттера, равной N_Э = 10¹⁷ см^-3 , диаметром эмиттера d_Э = 0,3 мм (S_Э = 0,07 мм² ), толщиной базы W = 10 мкм и концентрацией у коллектора N_К = 10¹⁴ см^-3 .

Предельная частота ƒ_β такого триода будет равна (на основании предыдущего примера)

ƒ_β = ƒ_β0 · 6=1700/100=17·6 ≈100 Мгц.

Удельная емкость эмиттерного перехода

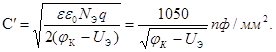
Емкость эмиттерного перехода может быть найдена из соотношения[5]