Курсовая работа: Двойственность в линейном программировании

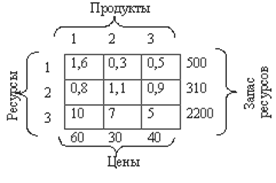
Рис. 3

2.2 Построение математической модели

Теперь приступим к созданию математической модели, т.е. к математической записи задачи.

Целевая функция:

Ограничения:

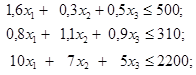
x ₁ ³ 0;

x ₂ ³ 0;

x ₃ ³ 0.

2.3 Описание решения данной задачи

Решим поставленную выше задачу с применением EXCEL.

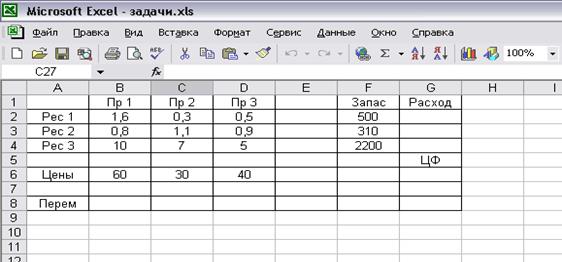
Содержание ячеек:

B1:D1 – имена продуктов (технологических способов);

A2:A4 – имена ресурсов;

B2:D4 – технологические коэффициенты (расход ресурсов при единичных интенсивностях технологических способов);

B6:D6 – цены продуктов;

B8:D8 – переменные;

F2:F4 – запас ресурсов;

G2:G4 – плановые расходы ресурсов, получаются в результате решения;

G6 – значение целевой функции, получается в результате решения.

Формулы для вычислений:

G2=СУММПРОИЗВ (B$8:D$8; B2:D2);

G3:G4 – копируются из G2;

G6=СУММПРОИЗВ (B8:D8; B6:D6).

Запишем формулы в ячейки G2:G4. Установить курсор на G2. На панели инструментов выбрать значок формул (f ). Появятся два окна. В окне «категория» выбрать «математические», затем в окне «функция» выбрать «СУММПРОИЗВ». Появится окно «СУММПРОИЗВ». В нем нужно указать, где располагаются операнды. Первый операнд – строка B$8:D$8, второй операнд – стока B2:D2. В ячейки G3:G4 формулу скопировать из G2. Аналогичным образом записать формулу целевой функции в ячейку G6. Теперь нужно указать остальные условия решения задачи. Установить курсор на ячейку целевой функции G6. В главном меню выбрать «сервис», а потом «поиск решения». Появится окно, в котором нужно указать:

1. Целевая ячейка – G6;