Курсовая работа: Экономико-статистический анализ эффективности производства зерна в сельскохозяйственных предприя

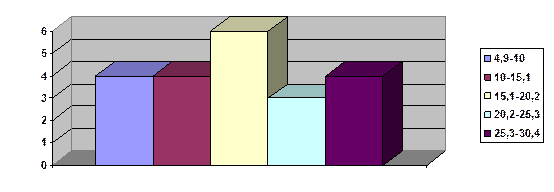
Рисунок 1 – Гистограмма распределения хозяйств по урожайности зерновых

Для выявления характерных черт, свойственных ряду распределения единиц, используем следующие показатели.

1) для характеристики центральной тенденции распределения определим среднюю арифметическую, моду, медиану признака.

Средняя величина признака определяется по формуле средней арифметической взвешенной: 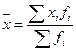, где - варианты; - средняя величина признака; - частоты распределения. В интервальных рядах в качестве вариантов () используют серединные значения интервалов.

ц/га

Мода – наиболее часто встречающееся значение признака, определяемое по формуле: , где - нижняя граница модального интервала; - величина интервала; - разность между частотой модального и домодального интервала; - разность между частотой модального и послемодального интервала.

ц/га

Медиана – значение признака, находящегося в центре ранжированного ряда распределения, определяемое по формуле: , где - нижняя граница медиального интервала; - величина интервала; - сумма частот распределения; - сумма частот домедиальных интервалов; - частота медиального интервала.

ц/га

2) для характеристики меры рассеяния признака определим показатели вариации.

Размах вариации составит: ц/га

Дисперсия составит:

Среднее квадратическое отклонение признака в ряду распределения составит: ц/га

Коэффициент вариации составит:

3) для характеристики формы распределения используем коэффициенты асимметрии () и эксцесса ():

Т.к. >0, распределение имеет правостороннюю асимметрию, о которой также можно судить на основе следующего неравенства: <<

Т.к. <0, фактическое (эмпирическое) распределение является низковершинным по сравнению с нормальным распределением. Если же >0 распределение следует признать высоковершинным по сравнению с нормальным (при нормальном распределении =0).

Определим величину показателей вариации и характеристик форм распределения на основе предварительных расчетных данных, представленных в таблице 9.

Таблица 9- Расчетные данные для определения показателей вариации, асимметрии и эксцесса

Серединное значение интервала по урожайности, ц ( xi )	Число хозяйств ( fi )	Отклонения от = 17,4(ц/га)
		()
7,45	4	-9,95	396,01	-3940,30	39205,99
12,55	4	-4,85	94,09	-456,34	2213,25
17,65	6	0,25	0,38	0,10	0,03
22,75	3	5,35	85,87	459,40	2457,79
27,85	4	10,45	436,81	4564,66	47700,70
Итого	21	×	1013,16	627,52	91577,76

1) Дисперсия: 48,245

2) Среднее квадратическое отклонение: ц/га

3) Коэффициент вариации:

4) Коэффициент асимметрии: 0,089

5) Эксцесс: -1,127