Курсовая работа: Формирование инвестиционного портфеля

причем в разложении

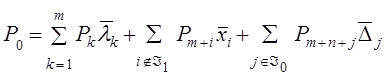(3.6.2)

коэффициент . Пусть также для множества индексов

существует оптимальный вектор для задачи (3.5.1), причем такой, что он не является допустимым для исходной задачи (3.1.2), т.е.

Тогда, если x¹ - оптимальная точка задачи (3.5.1) на многообразии X _{Á 1} , то Á ₁ порождает базис U_{Á 1} , а оптимальная точка x¹ принадлежит прямой (3.5.15):

(3.6.3)

Доказательство. Разложим вектор P₀ по базису U_{Á 1} , а вектор P_m+n+r по базису U_{Á 1, Á 0} :

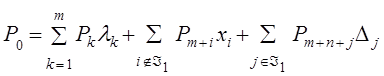
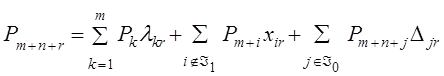
подставляя второе выражение в первое, и учитывая определение прямой (3.5.15) получаем очевидное следствие:

Кроме того, учитывая разложение (3.6.2), получаем, что

(3.6.4)

А согласно лемме 2, имеем:

Отсюда и из условия теоремы следует, что

Отсюда и из (3.6.4) вытекает доказываемое неравенство. Кроме того, из (3.6.4) также следует отличие от нуля коэффициента , что приводит к выводу о линейной независимости системы векторов U_{Á 1} . Это доказывает второе утверждение теоремы.

Теорема 2 указывает направление перехода от одного многообразия к другому с помощью операции Б, утверждая положит?