Курсовая работа: Градиентный метод первого порядка

Наряду с определением направления градиентного вектора основным вопросом, решаемым при использовании градиентных методов, является выбор шага движения по градиенту. Величина шага в направлении gradF в значительной степени зависит от вида поверхности. Если шаг слишком мал, потребуются продолжительные расчеты; если слишком велик, можно проскочить оптимум. Размер шага должен удовлетворять условию, при котором все шаги от базисной точки лежат в том же самом направлении, что и градиент в базисной точке. Размеры шага по каждой переменной x_i вычисляются из значений частных производных в базовой (начальной) точке:

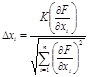, (6)

где К – константа, определяющая размеры шага и одинаковая для всех i-х направлений. Только в базовой точке градиент строго ортогонален к поверхности. Если же шаги слишком велики в каждом i-м направлении, вектор из базисной точки не будет ортогонален к поверхности в новой точке.

Если выбор шага был удовлетворительным, производная в следующей точке существенно близка к производной в базисной точке.

Для линейных функций градиентное направление не зависит от положения на поверхности, для которой оно вычисляется. Если поверхность имеет вид

то

и компонента градиента в i-м направлении равна

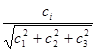. (7)

Для нелинейной функции направление градиентного вектора зависит от точки на поверхности, в которой он вычисляется.

Несмотря на существующие различия между градиентными методами, последовательность операций при поиске оптимума в большинстве случаев одинакова и сводится к следующему:

а) выбирается базисная точка;

б) определяется направление движения от базисной точки;

в) находится размер шага;

г) определяется следующая точка поиска;

д) значение целевой функции в данной точке сравнивается с ее значением в предыдущей точке;

е) вновь определяется направление движения и процедура повторяется до достижения оптимального значения.

Градиентный метод первого порядка

При оптимизации методом градиента оптимум исследуемого объекта ищут в направлении наиболее быстрого возрастания (убывания) выходной переменной, т.е. в направлении градиента. Но прежде чем сделать шаг в направлении градиента, необходимо его рассчитать. Градиент можно рассчитать либо по имеющейся модели

grad y(X)= ,

моделирование динамический градиентный полиномиальный

где - частная производная по i-му фактору;

i, j, k – единичные векторы в направлении координатных осей факторного пространства, либо по результатам n пробных движений в направлении координатных осей.

Если математическая модель статистического процесса имеет вид линейного полинома, коэффициенты регрессии b_i которого являются частными производными разложения функции y = f(X) в ряд Тейлора по степеням x_i , то оптимум ищут в направлении градиента с некоторым шагом h_i :

пкфв н(Ч)= и₁ р₁ +и₂ р₂ +…+и_т р_т

Направление корректируют после каждого шага.

Метод градиента вместе с его многочисленными модификациями является распространенным и эффективным методом поиска оптимума исследуемых объектов. Рассмотрим одну из модификаций метода градиента – метод крутого восхождения.

Метод крутого восхождения, или иначе метод Бокса-Уилсона, объединяет в себе достоинства трех методов - метода Гаусса-Зейделя, метода градиентов и метода полного (или дробного) факторного экспериментов, как средства получения линейной математической модели. Задача метода крутого восхождения заключается в том, чтобы шаговое движение осуществлять в направлении наискорейшего возрастания (или убывания) выходной переменной, то есть по grad y(X). В отличии от метода градиентов, направление корректируется не после каждого следующего шага, а при достижении в некоторой точке на данном направлении частного экстремума целевой функции, как это делается в методе Гаусса-Зейделя. В точке частного экстремума ставится новый факторный эксперимент, определяется математическая модель и вновь осуществляется крутое восхождение. В процессе движения к оптимуму указанным методом регулярно проводиться статистический анализ промежуточных результатов поиска. Поиск прекращается, когда квадратичные эффекты в уравнении регрессии становятся значимыми. Это означает, что достигнута область оптимума.

Опишем принцип использования градиентных методов на примере функции двух переменных